力扣上一道中等题,求两个字符串的最长公共子序列。说实话这道题我完全没有思路,一开始尝试用双指针去遍历两个数组,但是公共子序列可以是不连续的,这样情况就会变得很复杂。在和力扣度过美好的一天后,我最终放弃了。看完题解后,茅塞顿开。故此记录一下思考过程
题目
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,”ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。示例 2:
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc" ,它的长度为 3 。示例 3:
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0 。思路
解题方法还是(动态规划) O(nm) 。给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度 (子序列可以不连续)。
样例:
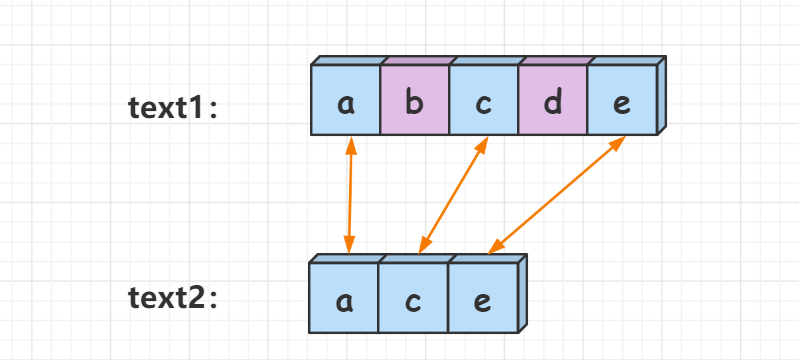
如样例所示,字符串abcde与字符串ace的最长公共子序列为ace,长度为3。最长公共子序列问题是典型的二维动态规划问题,下面来讲解动态规划的做法。
状态表示:
定义 f[i][j]表示字符串text1的[1,i]区间和字符串text2的[1,j]区间的最长公共子序列长度(下标从1开始)。
状态计算:
可以根据text1[i]和text2[j]的情况,分为两种决策:
若
text1[i] == text2[j],也就是说两个字符串的最后一位相等,那么问题就转化成了字符串text1的[1,j-1]区间和字符串text2的[1,j-1]区间的最长公共子序列长度再加上一,即f[i][j]=f[i - 1][j - 1]+ 1。(下标从1开始)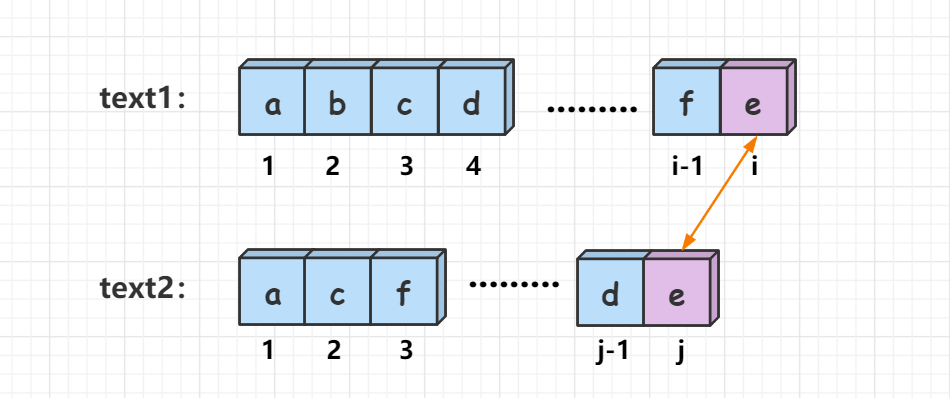
若
text1[i] != text2[j],也就是说两个字符串的最后一位不相等,那么字符串text1的[1,i]区间和字符串text2的[1,j]区间的最长公共子序列长度无法延长,因此f[i][j]就会继承f[i-1][j]与f[i][j-1]中的较大值,即f[i][j]= max(f[i-1][j],f[i][j-1]) 。 ( 下标从1开始)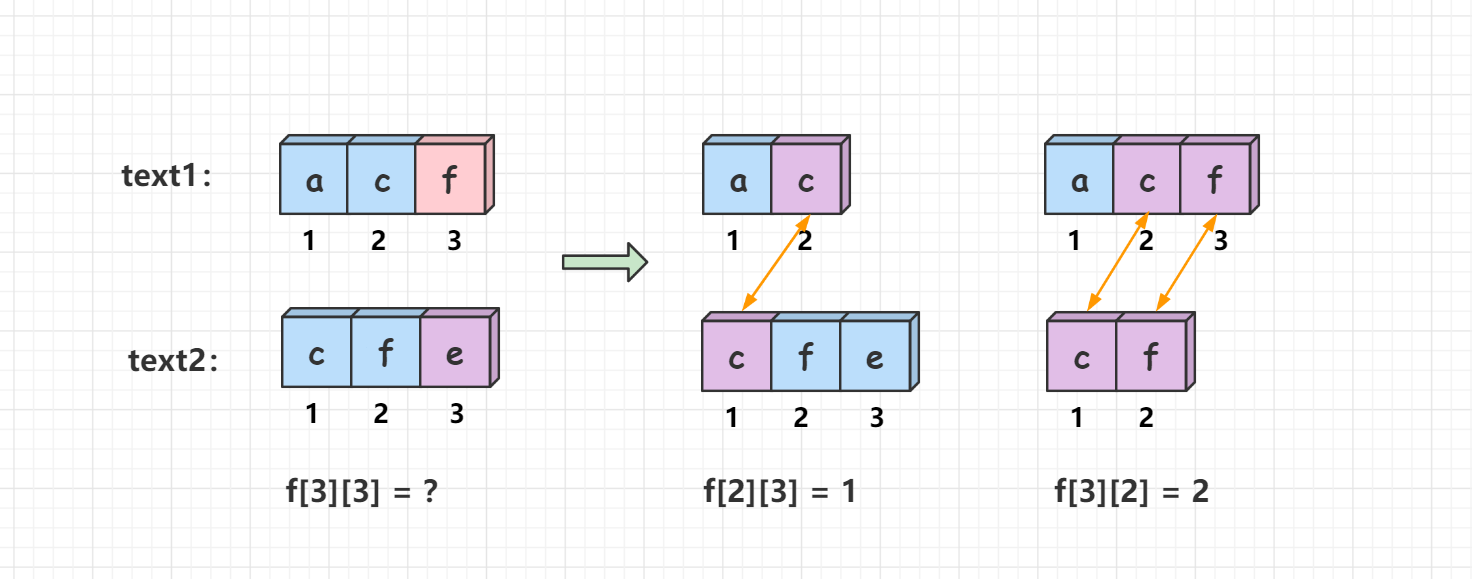
如上图所示:我们比较
text1[3]与text2[3],发现’f’不等于’e’,这样f``[3][3]无法在原先的基础上延长,因此继承”ac”与”cfe” ,”acf”与”cf”的最长公共子序列中的较大值,即f[3][3]= max(f[2][3],f[3][2]) = 2。
因此,状态转移方程为:
f[i][j] = f[i-1][j-1] + 1 ,当text1[i] == text2[j]
f[i][j] = max(f[i - 1][j],f[i][j - 1]),当text1[i] != text2[j]
初始化:
f[i][0] = f[0][j] = 0,(0 <=i<=n, 0<=j<=m)空字符串与有长度的字符串的最长公共子序列长度肯定为0。
实现细节
我们定义的状态表示f数组和text数组下标均是从1开始的,而题目给出的text数组下标是从0开始的,为了一 一对应,在判断text1和text2数组的最后一位是否相等时,往前错一位,即使用text1[i - 1]和text2[j - 1]来判断。
这里解释一下为什么f数组和text数组均定义成下标从1开始。原因是因为状态转移方程 f [i] [j] = max(f [i - 1] [j], f [i] [j - 1]), 当我们的f数组定义成下标从1开始以后,我们就可以在代码中不用对下标越界问题做出额外判断。其实我们也可以发现一个问题,就是题目给定的原数组,比如text数组,如果下标从1开始的话,状态表示会更加的清晰,推导状态转移方程的过程也会更加好理解。
时间复杂度分析: O(nm),其中n 和 m 分别是字符串 text1 和 text2的长度。
Java代码实现
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int n = text1.length(), m = text2.length();
int[][] f = new int[n + 1][m + 1];
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
f[i][j] = f[i - 1][j - 1] + 1;
} else {
f[i][j] = Math.max(f[i - 1][j], f[i][j - 1]);
}
}
}
return f[n][m];
}
}
本文解题思路参考地址,我觉写得比官方题解更清晰易懂。动态规划最难的点还是找出转移方程,加油吧。



