LeetCode-八皇后问题

八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。 高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。计算机发明后，有多种计算机语言可以解决此问题。—-节选自百度百科

在力扣与八皇后对应的题目是N皇后问题

N 皇后

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

示例 1：

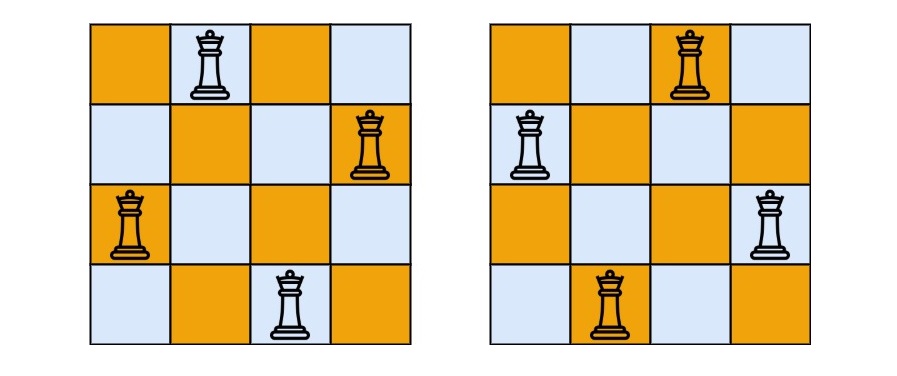
输入：n = 4
输出：[ [“.Q..”,”…Q”,”Q…”,”..Q.”] , [“..Q.”,”Q…”,”…Q”,”.Q..”] ]
解释：如上图所示，4 皇后问题存在两个不同的解法。

算法思路

对于八皇后问题我脑海第一想到的思路，就是自己维护一个 8×8 矩阵，每次找到一个空位摆下一个皇后就把对应行列对角线上的棋格做个标记，后面摆皇后的时候通过这个矩阵判断一下，没有标记的位置就可以摆，但这种方式时间复杂度比较高，每次摆皇后需要遍历一下矩阵，同时需要额外操作维护这个矩阵。虽然我第一想到的是通过矩阵维护状态，但是马上又舍弃了这种思路，因为对DFS有一定的了解，对于这个题肯定有更好的解法那就是回溯（虽然之前也看过回溯算法的思路和技巧，但八皇后问题算是我正儿八经的使用回溯算法解的第一道题了）。来看看回溯的思路，我们试想一下简单点的四皇后问题，如果有一个4×4的棋盘，直接去摆皇后的话，会怎么操作：

1. 在第一行的第一个格子摆一个皇后
2. 在第二行的每个格子尝试摆皇后，只要不同列，不同斜线上就可以摆
3. 在第三行重复步骤2的操作，如果第三行没有可以摆的位置怎么办，那说明前面两行摆皇后的位置不对，导致无解。我们回到第二行，重新调整皇后的位置，再往下继续摆。如果第二行的所有格子都摆完了，我们再回到第一行，调整第一行皇后的位置，继续摆。（这种方式就叫回溯，这里没有举例第四行，其实同理第三行的步骤）

回溯法在碰到摆不下去的情况，会回到上一行，摆下一个格子，然后继续往下走。实际上穷举了所有情况，和8个for循环差不多，只是在代码实现上更简单。回溯法经典的实现方式是使用递归，一般来说使用函数递归，即编译器的递归函数，但是其性能令人遗憾，但某些递归可以转化为迭代

我们知道递归和迭代一定程度上是可以很容易做到互相转化实现同样的思路的。递归是重复调用函数自身实现循环，迭代是函数内某段代码实现循环，使用递归的话我们应该要有一个能在第N行找到某一列的格子可以放皇后的函数，能找到把参数+1去调用自己去找下一行皇后能放的格子，找不到就算了。如果想用迭代，前面我们说过递归迭代是可以转化的，这种在函数最后调用自己的递归更是极易转化，我们按着迭代的套路在for循环的里按照刚刚递归的思路加几个判断判别循环是continue、break还是返回前一层循环即可。最后还有一种思路，准确来说还是和递归脱离不了关系，学习递归的时候我们我们知道，递归可以看做底层帮你维护的一个堆栈不断地push、pop，知道它的本质我们也可以通过手动维护一个堆栈来模拟这个递归调用的过程，只要构造两个函数backward(往后回溯)、refresh(向前刷新)来模拟堆栈进出即可。

最后我们来分析三个方法（递归法、迭代法、手动堆栈法）表现和改进，很明显在代码量上递归会是最短的，这里所有的算法都是一行一行的摆Q，这样保证了所有的Q不会同行，因此只需考虑Q在同列，同斜线的情况

递归法

class Solution {
    public List<List<String>> solveNQueens(int n) {
        List<Integer[]> res = new ArrayList<>();
        int[] ans = new int[n];
        for(int i=0;i<n;i++){
            ans[i]=-1;
        }
        // 从第0行开始摆Q
        getQueensRes(0,n,ans,res);
        // 打印结果
        List<List<String>> result = new ArrayList<>();
        for(Integer[] ins : res){
            List<String> list = new ArrayList<>();
            for(int i=0;i<ins.length;i++){
                StringBuilder sb = new StringBuilder();
                for(int j=0;j<ins.length;j++){
                    if(ins[i]==j){
                        sb.append('Q');
                    }else {
                        sb.append('.');
                    }
                }
                list.add(sb.toString());
            }
            result.add(list);
        }
        return result;
    }

    private void getQueensRes(int row,int n,int[] ans,List<Integer[]> res){
        for(int j=0;j<n;j++){
            // 当前位置可摆Q
            if(canPutQueen(row,j,ans)){
                ans[row]=j;
                // 到达最后一行,说明所有行已经找完了,已经找到一种结果
                if(row==n-1){
                    // 记录结果
                    Integer[] ins = new Integer[n];
                    for(int i=0;i<ans.length;i++){
                        ins[i]=ans[i];
                    }
                    res.add(ins);
                    ans[row]=-1;
                    return;
                }
                // row+1 继续下一行找可以摆Q的位置
                getQueensRes(row+1,n,ans,res);
            }
        }
        // 回溯,重置上一行状态
        // 当前行没有找到可以摆Q的位置,说明上一行摆的不对,回溯到上一行重新摆
        // 判断一下row>0，因为第0行没有上一行
        if(row>0){
            ans[row-1]=-1;
        }
    }

    // 判断当前位置摆Q是否和前面摆过的Q位置有冲突
    private boolean canPutQueen(int row,int col,int[] ans){
        // 和前面摆过的Q比较
        for(int i=0;i<row;i++){
            // 同列
            if(ans[i]==col){
                return false;
            }
            // 同斜线
            if(Math.abs(ans[i]-col)==Math.abs(i-row)){
                return false;
            }
        }
        return true;
    }
}

递归法不多说了，八皇后的最标准解法，我的注释也很详细。结合我前面说的四皇后摆Q的思路就很好理解了

迭代法

class Solution {
    // 8皇后 迭代法
    public List<List<String>> solveNQueens2(int n) {
        List<List<String>> result = new ArrayList<>();
        if(n==1){
            List<String> list = new ArrayList<>();
            list.add("Q");
            result.add(list);
            return result;
        }
        List<Integer[]> res = new ArrayList<>();
        int j=0;
        // 定义一个数组维护前面的行摆过的Q的位置,没有摆过则初始化为-1
        int[] ins = new int[n];
        for(int i=0;i<n;i++){
            ins[i]=-1;
        }
        for(int i=0;i<n;i++){
            // i在第0行回溯的时候会得到-1,这说明第0行也没找到可以摆Q的位置了
            // 按理来说这是不可能的,第0行可以随便摆。那只能说明第0行已经遍历完了,所有情况已经枚举完了
            if(i==-1){
                break;
            }
            // 这里可能是回溯回来的，所以从第i行的下一个格子开始找
            j=ins[i]+1;
            // 因为可能是回溯回来的,把当前位置的状态置为-1,即没有摆过Q
            ins[i]=-1;
            for(;j<n;j++){
                // 如果当前位置可以摆Q
                if(canPutQueen2(i,j,ins)){
                    ins[i]=j;
                    // 如果已经到达最后一行，说明已经找到一种摆放的结果
                    if(i==n-1){
                        //记录结果
                        Integer[] rs = new Integer[n];
                        for(int k=0;k<n;k++){
                            rs[k]=ins[k];
                        }
                        res.add(rs);
                        ins[i]=-1;
                        // 回到上一行找其他可能的结果
                        // 因为循环时i++ ,所以 i-2 回到上一行
                        i=i-2;
                        break;
                    }
                    // 走到这里说明第i行的第j格子可以摆Q,跳出循环到下一行继续摆Q
                    break;
                }
            }
            // 判断当前行有没有摆Q,如果没有摆则说明上一行摆的不对,回溯到上一行
            if(ins[i]==-1){
                i=i-2;
            }
        }

        for(Integer[] integers : res){
            List<String> list = new ArrayList<>();
            for (Integer integer : integers) {
                StringBuilder sb = new StringBuilder();
                for (int m = 0; m < integers.length; m++) {
                    if (integer == m) {
                        sb.append('Q');
                    } else {
                        sb.append('.');
                    }
                }
                list.add(sb.toString());
            }
            result.add(list);
        }
        return result;
    }

    private boolean canPutQueen2(int row,int col,int[] ans){
        // 和前面摆过的Q比较
        for(int i=0;i<row;i++){
            // 同列
            if(ans[i]==col){
                return false;
            }
            // 同斜线
            if(Math.abs(ans[i]-col)==Math.abs(i-row)){
                return false;
            }
        }
        return true;
    }
}

迭代法是按用迭代的套路来完成递归的思路的一个解法。当你写出迭代法后，可以按照迭代的思路把迭代转为递归实现。

堆栈法

手动维护堆栈对于我们理解递归本质是很有好处的，递归调用的本质是我们利用编程语言的特性，可以看做底层帮你维护的一个堆栈不断地push、pop，实际上我们也可以通过手动维护一个栈来模拟这个递归调用的过程。

class Solution {
    // 8皇后 堆栈法
    public List<List<String>> solveNQueens3(int n) {
        List<Integer[]> res = new ArrayList<>();
        Stack<Queen> stack = new Stack<>();
        // 用数组来维护皇后的位置
        int[] ans = new int[n];
        // 初始化为-1
        for(int i=0;i<n;i++){
            ans[i]=-1;
        }
        // 从第0行第0列开始摆
        stack.add(new Queen(0,0));

        while (!stack.isEmpty()){
            Queen queen = stack.peek();
            // 如果当前位置可以摆Q
            if(canPutQueen3(queen.row,queen.col,ans)){
                ans[queen.row]=queen.col;
                // 判断是否到达最后一行
                if(queen.row==n-1){
                    // 记录结果
                    Integer[] ins = new Integer[n];
                    for(int i=0;i<n;i++){
                        ins[i]=ans[i];
                    }
                    res.add(ins);
                    // 弹出顶层皇后,回溯到上一行
                    stack.pop();
                    // 可能当前行是第0行,stack会为空
                    if(stack.isEmpty()){
                        break;
                    }
                    // 把上一行的Q移动到下一个col继续摆
                    Queen temp = stack.peek();
                    temp.col=temp.col+1;
                    // 重置位置
                    ans[temp.row]=-1;
                    continue;
                }
                // 移动找下一行继续摆
                stack.add(new Queen(queen.row+1,0));
            }else {
                // 如果col=n说明这行的所有col已经遍历完且都不能摆,说明上一行的Q摆的不对,需要回溯到上一行,并从下一个col开始继续尝试
                if(queen.col==n){
                    // 把当前行的Q弹出,回溯到上一行
                    stack.pop();
                    if(stack.isEmpty()){
                        break;
                    }
                    // 把上一行的Q移动到下一个col继续摆
                    Queen temp = stack.peek();
                    temp.col=temp.col+1;
                    // 重置位置
                    ans[temp.row]=-1;
                    continue;
                }
                //当前行继续找下一个col
                queen.col=queen.col+1;
            }
        }
        List<List<String>> result = new ArrayList<>();
        for(Integer[] integers : res){
            List<String> list = new ArrayList<>();
            for (Integer integer : integers) {
                StringBuilder sb = new StringBuilder();
                for (int m = 0; m < integers.length; m++) {
                    if (integer == m) {
                        sb.append('Q');
                    } else {
                        sb.append('.');
                    }
                }
                list.add(sb.toString());
            }
            result.add(list);
        }
        return result;

    }

    private boolean canPutQueen3(int row,int col,int[] ans){
        if(row==ans.length || col==ans.length){
            return false;
        }
        // 和前面摆过的Q比较
        for(int i=0;i<row;i++){
            // 同列
            if(ans[i]==col){
                return false;
            }
            // 同斜线
            if(Math.abs(ans[i]-col)==Math.abs(i-row)){
                return false;
            }
        }
        return true;
    }
}

class Queen {
    int row;
    int col;

    public Queen(int row,int col){
        this.row=row;
        this.col=col;
    }
}