异或是一种基于二进制的位运算,任何数和 0 做异或运算,结果仍然是原来的数,即 a ⊕ 0=a⊕0=a。
任何数和其自身做异或运算,结果是 0,即 a ⊕ a=0 a⊕a=0。简单理解就是两个 bit 位异或,如果两个 bit 位值相同则结果为0,如果两个 bit 位值不同则结果为1。异或运算满足交换律和结合律
交换律与结合律即1到1000的数字异或运算,如
1^2^...^n^...^m^...^1000,无论这n和m出现在什么位置,都可以转换成为1^2^...^1000^(n^m)的形式
leetcode上有很多关于位运算的算法题,如下题
题目
一个整型数组里除了两个数字之外,其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。
这是一道很新颖的关于位运算的面试题。首先我们简单的想法可能是创建一个Map<Integer, Integer>类型。它的键存放出现的数字,值是数字出现的次数。实现代码如下
public void nums(int[] array){
Map<Integer, Integer> map = new HashMap<>()
for(int i=0;i<array.length,i++){
Integer temp = map.get(array[i])
if(temp == null){
map.put(array[i],1)
}else{
map.put(array[i],temp+1)
}
}
for(Integer key:map.keySet()){
if(map.get(key)==1){
System.out.println(map.get(key))
}
}
}但是这样做的不满足题目给出的时间复杂度是O(n),空间复杂度是O(1)的要求。有没有什么办法使我们能直接在原数组上操作能得到结果呢?有的,就是使用异或。因为异或是相同为0,不同为1,异或是基于位运算的。所以在这个题中,相同的所有的数异或后依然为0, 最后异或的结果就是两个不同的数异或的结果,因为他们不同,所以按位异或后的结果数值的32bit里面肯定或有一位是1,而我们就找这其中一位异或结果是1的那个位为基准。将数组分成两个数组,那么分下来后两个不同的数肯定就分在两个数组中。说了这么多是不是有些不明白?其实我第一次看见这个的时候我一度不知道是什么意思,完全懵的状态。我用一个例子说话
a[] = {3,2,9,4,5,6,7,2,4,5,6,7};在这个数组中不同的两个数是9和3,这个数组通过异或运行后,其实就化成了9和3两个数的异或运算。因为异或满足交换律和结合律,所以数组中的值全部顺序异或即 3^2^9^4^5^6^7^2^4^5^6^7 可以转化为 (2^2)^(4^4)^(5^5)^(6^6)^(7^7)^(3^9) 而相同数字的异或结果为0,所以这个式子前面结果全是0,所以就变成了0^3^9而不同数字与0异或结果还是他本身,所以整个数组的异或其实结果就是 3^9
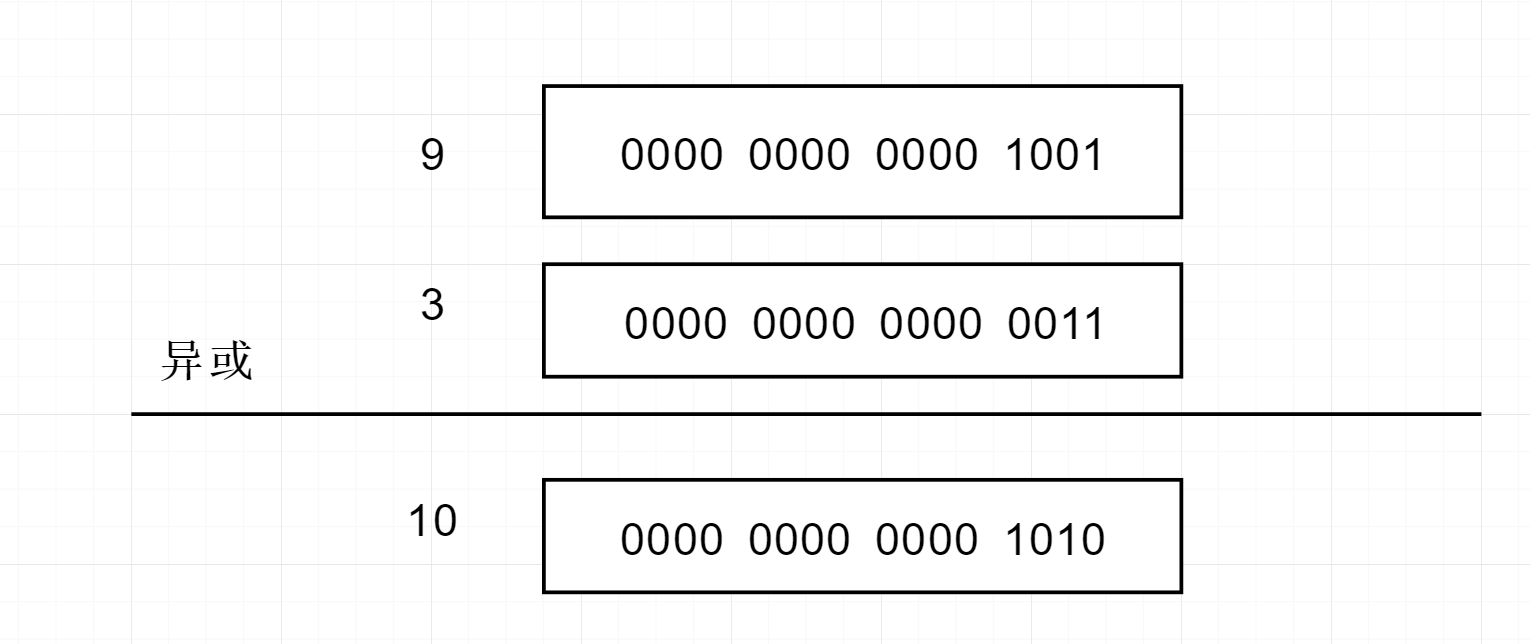
从上面结果可知异或结果为10; 其中在他们位中第1,3位结果为1;我们可以以其中任意一个位为基准进行数组分类。我们按最低位的bit为1位(即第二位)来作为我们的基准,第二位是0的作为一组,第二位是1的作为另一组。分出来的两个数组为第一组:{3,2,6,7,2,6,7}; 第二组{9,4,5,4,5};知道为什么这么分组了吗?,就是因为他们异或不相同,那么肯定有一位是不一样的,一个数的那位肯定为1, 另一个数肯定为0,最后转换为我们之前说的那个一个数组中找只有一个数是单数的问题了。对上面分出来的两个数组再分别进行一次异或运算即可找到两个数了
只出现一次的数字
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
解题思路:有了前一道题做铺垫,这个题就很简单了,遍历数组每个元素依次做异或返回结果即可



