在地铁上刷力扣时,无意中看到这个题。题目描述挺简单的,然后动脑想想感觉也挺简单的,但是实际动手写代码起来,却怎么运行怎么不对。最后花了两个下午才把它做出来,我的解题方式和官网提供的解题思路都不一样,自创解法,虽然能解题,但是思路不通用,感觉自己好菜,胆小可怜又无助 o(╥﹏╥)o 。话不多说,来看一下题目。
最长有效括号
给定一个只包含 '(' 和 ')' 的字符串,找出最长的包含有效括号的子串的长度。左口号和右括号能成对出现就算有效口号,看例子
示例1
输入: "(()"
输出: 2
解释: 最长有效括号子串为 "()"示例2
输入: ")()())"
输出: 4
解释: 最长有效括号子串为 "()()"示例3
输入: ")()(())"
输出: 6
解释: 最长有效括号子串为 "()(())"示例4
输入: ")(())()()(.))"
输出: 8
解释: 最长有效括号子串为 "(())()()"解题思路
对于这道题的解法,力扣上有很多思路,官方提供了三种解题思路,一种是用动态规划算法,第二种是用栈的方式解题,第三种是用两个指针计数遍历法。这里主要讲一下动态规划算法
动态规划实现
结合题目,有最长这个字眼,可以考虑尝试使用 动态规划 进行分析。这是一个 最值型 动态规划的题目。动态规划三步走,这里先定义dp[i] 数组表示以下标 i 字符结尾的最长有效括号的长度,然后我们先找状态转移方程。根据题意,显然有效的子串一定以 ‘)’ 结尾,因此我们可以知道以 ‘(‘ 结尾的子串对应的 dp 值必定为 0 ,我们只需要求解 ‘)’ 在 dp数组中对应位置的值。即当 s[i] = ‘(‘ 时,s[i] 无法和其之前的元素组成有效的括号对,所以dp[i] = 0。我们来看当 s[i] = ‘)’ 的情况,又分为以下两种子情况
情况1
当s[i−1]==′(′时:此时 s[i] 和 s[i - 1] 组成一对有效括号,有效括号长度新增长度2,i 位置对最长有效括号长度为 其之前2个位置的最长括号长度加上2,即形如 “……()” 的情况,我们可以推出状态方程: dp[i]=dp[i−2]+2
情况2
当s[i−1]==′)′时:这种情况下,如果前面有和s[i]s[i]组成有效括号对的字符,即形如 “……(())”,这样的话,就要求s[i - 1]位置必然是有效的括号对。这时,我们只需要找到和s[i]s[i]配对对位置,并判断其是否是 ‘(‘ 即可。和 i 位置配对对位置为 i- 1 - dp[i - 1],为什么是 i - 1 - dp[i - 1],这个有些难以理解,首先我们得知道 dp[i - 1] 的值是什么意思,dp[i-1]是在位置i-1处的最长有效括号长度,那么为什么与 i 对称的位置会是 i 减1 再减去 i-1 处的最长有效括号长度呢,这个关系式是比较难找的地方,直接看例子吧,多举几个例子就能找到规律。数学归纳法嘛,本质也是找规律
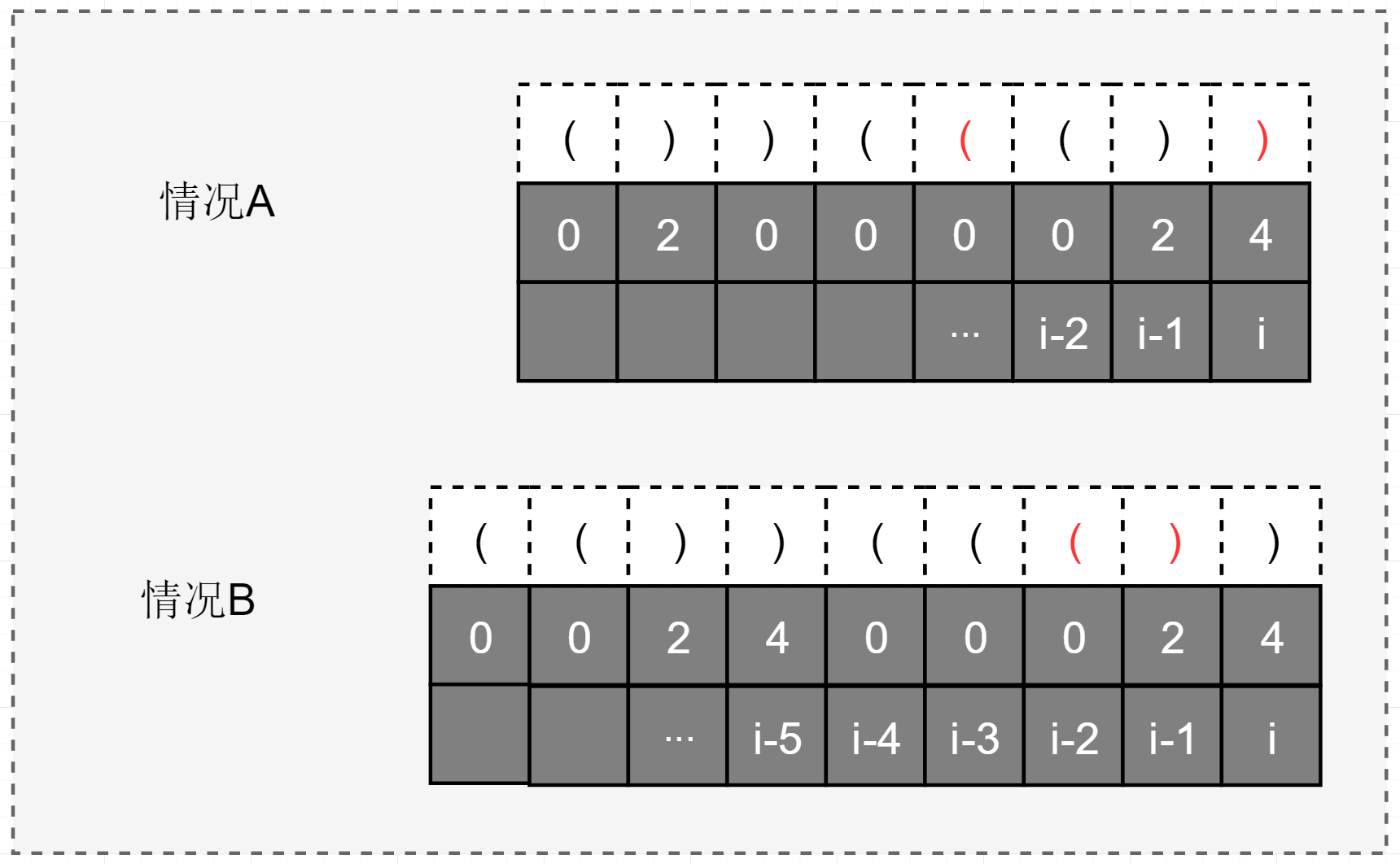
dp[i]保存的是在i处的最长有效括号长度,对于情况A很好理解,需要注意的是情况B,在i-1处保存的最长有效括号长度是2,而我之前的理解应该是4,因为4是最长的嘛。这种理解是错误的,长度4已经在前面保存过了,有效括号在i-4出中断了,然后会重新计数,因此在 i 处保存的是到 i 处有括号没有中断的最长长度。所以在 i-1 处有效括号长度是2。接下来就是重点了
- 以图中情况B为例,可以得出于 i 对应的左括号位置是 i-3,
- 而 i-3 = i-1-2 = i-1-dp[i-1] ,为什么能用 dp[i-2] 代替 i-1-2中的2,因为有效括号一定是对称的
- 所以得出与 i 位置对称的左括号位置是 i-1-dp[i-1]
现在我们来求状态转移方程,根据数学归纳法。为了便于理解,看下图
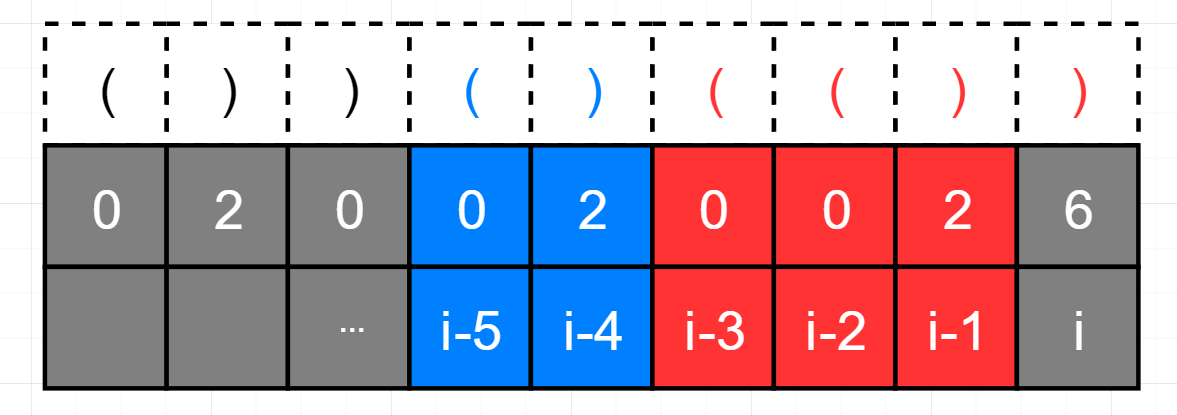
可以得出 dp[i]=dp[i-1]+dp[i-4]+2,我来解释一下这个方程,在 i 处的最长有效括号长度是由三部分组成的,即在 i-1处的最长有效括号长度,在 i-4 处的最长有效括号长度以及在 i 处如果是 ) 右括号那么最长有效括号长度加2,即dp[i-1] 是在i-1处的最长有效括号,也就是图中红色的方格,dp[i-4] 是在i-4处的最长有效括号图中蓝色的方格。而 dp[i-4] 中 i-4 就是 i 对应的左括号位置的前一个位置,即 i-3 的前一个位置,由前面我们已经算出 i-3 =i-1-dp[i-1] ,所以 dp[i] = dp[i-1]+dp[i-2-dp[i-1]]+2。好了,根据前面的分析,我们终于得到了如下两个计算公式:
dp[i]=dp[i−2]+2dp[i] = dp[i-1]+dp[i-2-dp[i-1]]+2
那么,求 dp[i] 就变成了求dp[i - 1]、 dp[i - 2]、dp[i - dp[i - 1] - 2] 的子问题。 现在完成了动态规划的两步了,找出了状态转移方程,定义了dp数组,还剩下一步就是初始条件和边界情况
初始条件: dp[i] = 0
边界情况:需要保证计算过程中:i - 2 >= 0 和 i - 2 - dp[i - 1] >= 0
动态规划最难的就是求出状态关系方程,这个解决了,剩下写代码的事情也就容易了。
我的实现
我看了题目后我的第一感觉是把所有可能的有效括号找出来,然后再逐个求 length 继而求出最长的有效括号。虽然这样求出了最长括号但是却多占用了一些空间复杂度,因为我不仅仅求了长度,还把有效括号这个字符串本身也找出来了。
解题思路
看到这个题时我想到的是从左往右遍历字符串,然后定义一个计数变量 index ,每当遇到 ( 左括号则 index+1,每当遇到 ) 右括号则 index-1 ,当index==0时,说明找了一个有效括号,这样只需要遍历完字符串,就可以找到所有的有效括号,然后比较找出最长的有效括号即可。大致思路是如此,但实际写代码要考虑很多边界问题,最后代码实现如下
public int longestValidParentheses(String s) {
StringBuilder temp = new StringBuilder(s);
s= s+temp.reverse().toString();
char[] chars = s.toCharArray();
boolean isContact = true;
StringBuilder sb = new StringBuilder();
String target="";
int index=0;
char kh1 = '(',kh2=')';
for(int i=0;i<chars.length;i++){
if(i==chars.length/2){
sb = new StringBuilder();
index=0;
isContact = false;
kh1 = ')';
kh2 = '(';
}
if(kh1 == chars[i]){
sb.append(chars[i]);
isContact = true;
index++;
}else{
if(kh2 == chars[i] && sb.length()>0){
sb.append(chars[i]);
index--;
if(index==0 && sb.length() > target.length()){
if(isContact){
target = sb.toString();
if(i>=chars.length/2){
target = new StringBuilder(target).reverse().toString();
}
}else {
sb = new StringBuilder();
}
}else if(index < 0){
index = 0;
isContact = false;
sb = new StringBuilder();
}
}else {
sb = new StringBuilder();
index=0;
isContact = false;
}
}
}
return target.length();
}入参 s 是待求解的字符串,例如传入 ())()(()),则会返回 6 ,因为最长有效括号是 ()(())。其中第47行的 target 就是目标字符串,即最长有效括号



