LeetCode-迷宫问题

上篇说到广度优先搜索算法，今天就来做一个应用广度优先算法的力扣算法题吧。这个题是力扣上很常见的求最短路径类型的算法题，对于这种题如果没有解题的算法思路，看到题基本就是脑子一片空白，无从下手的关键。但是使用广度优先搜索算法去求解它时，代码实现却非常简单。

迷宫

题目：给一个二维列表，表示迷宫（0表示通道，1表示围墙）。起点坐标[x=1,y=0]；终点坐标[x=9,y=8]。给出算法，求一条走出迷宫的最短路径。其中x表示横坐标，y表示纵坐标。

    private static int[][] maze = {
            {1,1,1,1,1,1,1,1,1,1},
            {0,0,0,1,0,0,0,1,0,1},
            {1,0,0,1,0,0,0,1,0,1},
            {1,0,0,0,0,1,1,0,0,1},
            {1,0,1,1,1,0,0,0,0,1},
            {1,0,0,0,1,0,0,0,0,1},
            {1,0,1,0,0,0,1,0,0,1},
            {1,0,1,1,1,0,1,1,0,1},
            {1,1,0,0,0,0,0,0,0,1},
            {1,1,1,1,1,1,1,1,0,1}
    };

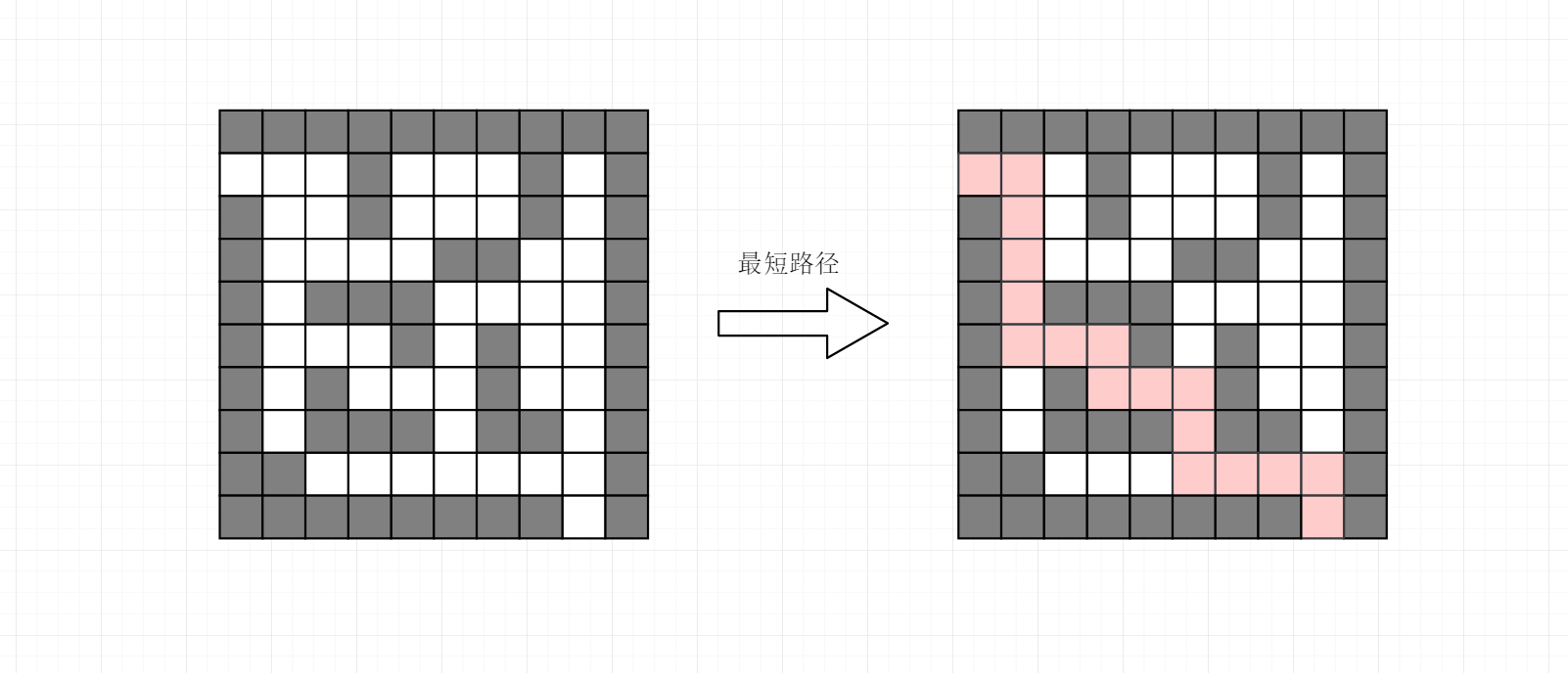
为了更好理解，对应的迷宫的图如下，其中黑色代表墙，白色代表通道。红色是一条最短路径

解题思路

解题思路不多说了，使用广度优先搜索算法即可找到最短迷宫路径。

代码实现

Java版本

package com.example.maze;

import java.util.ArrayList;
import java.util.List;

/**
 * @Auther: Lushunjian
 * @Date: 2020/5/28 22:12
 * @Description:
 */
public class MazeTest {

    private static int[][] maze = {
            {1,1,1,1,1,1,1,1,1,1},
            {0,0,0,1,0,0,0,1,0,1},
            {1,0,0,1,0,0,0,1,0,1},
            {1,0,0,0,0,1,1,0,0,1},
            {1,0,1,1,1,0,0,0,0,1},
            {1,0,0,0,1,0,0,0,0,1},
            {1,0,1,0,0,0,1,0,0,1},
            {1,0,1,1,1,0,1,1,0,1},
            {1,1,0,0,0,0,0,0,0,1},
            {1,1,1,1,1,1,1,1,0,1}
    };
    private static Node startNode = new Node(null,0,1,0);
    private static Node endNode = new Node(null,0,9,8);

    // 1:墙   0:路   10*10 = x*y
    /**
     * 上：maze[x-1][y]
     * 下：maze[x+1][y]
     * 左：maze[x][y-1]
     * 右：maze[x][y+1]
     * */
    public static void main(String[] args){
        List<Node> list = new ArrayList<>();
        list.add(startNode);
        Node node = getPath(list);
        while (true){
            System.out.println("x:"+node.getCoX()+"--y:"+node.getCoY());
            node = node.getPreNode();
            if(node == null)
                break;
        }
    }

    private static Node getPath(List<Node> nodeList){
        List<Node> nextNodes = new ArrayList<>();
        for(Node node : nodeList){
            maze[node.getCoX()][node.getCoY()] = 1;
            nextNodes.addAll(getNextNodes(node));
        }
        for(Node node : nextNodes){
            if(node.getCoX() == endNode.getCoY() && node.getCoY() == endNode.getCoY()){
                return node;
            }
        }
        return getPath(nextNodes);
    }

    // 返回节点的下一个可达节点集合
    private static List<Node> getNextNodes(Node node){
        int x = node.getCoX();
        int y = node.getCoY();
        List<Node> nextNodes = new ArrayList<>();
        // 如果向下不越界，且下方不是墙
        if(x<maze.length && maze[x+1][y] ==0)
            nextNodes.add(new Node(node,maze[x+1][y],x+1,y));
        if(y<maze[0].length && maze[x][y+1] == 0)
            nextNodes.add(new Node(node,maze[x][y+1],x,y+1));
        if(x>0 && maze[x-1][y] == 0)
            nextNodes.add(new Node(node,maze[x-1][y],x-1,y));
        if(y>0 && maze[x][y-1]==0)
            nextNodes.add(new Node(node,maze[x][y-1],x,y-1));
        return nextNodes;
    }


    static class Node{
        private Node preNode;
        private int value;
        private int coX;
        private int coY;

        public Node(Node preNode, int value, int coX, int coY) {
            this.preNode = preNode;
            this.value = value;
            this.coX = coX;
            this.coY = coY;
        }

        public Node getPreNode() {
            return preNode;
        }

        public void setPreNode(Node preNode) {
            this.preNode = preNode;
        }

        public int getValue() {
            return value;
        }

        public void setValue(int value) {
            this.value = value;
        }

        public int getCoX() {
            return coX;
        }

        public void setCoX(int coX) {
            this.coX = coX;
        }

        public int getCoY() {
            return coY;
        }

        public void setCoY(int coY) {
            this.coY = coY;
        }
    }
}