广度优先搜索算法BFS

最近在看到力扣上一道推箱子算法题时，思考了很久也想不到解题思路。于是查了一下推箱子的解题思路，便查到了广度优先搜索算法（BFS），广度优先搜索算法专门用于解决最短路径问题，其算法思路也很简单。而推箱子问题就可以用广度搜索算法解决，与它类似的问题还有，迷宫出口问题，最佳距离问题等。与广度优先搜索算法对应的还有深度优先搜索算法，深度优先搜索算法主要解决广度搜索算法空间复杂度高的问题，但是深度优先搜索算法它只能找到有解，无法找到最短路径。本文主要总结一下广度优先搜索算法

推箱子

我以推箱子问题开始吧，推箱子相信大家都玩过，小时候电视机上或者手机上都有内置游戏，一般就有推箱子。推箱子问题如下，游戏地图用大小为 n * m 的网格 grid 表示，其中每个元素可以是墙、地板或者是箱子。现在你将作为玩家参与游戏，按规则将箱子 B 移动到目标位置 T，板用字符 '.' 表示，意味着可以自由行走，墙用字符 '#' 表示，意味着障碍物，不能通行。地图如下

[
 ["#","#","#","#","#","#"],
 ["#","T","#","#","#","#"],
 ["#",".",".","B",".","#"],
 ["#",".","#","#",".","#"],
 ["#",".",".",".","S","#"],
 ["#","#","#","#","#","#"]
]

问箱子推到目标地点的最小推动次数。当我看到这个题时，我是懵的，脑海中完全想不出一种可以用代码表示出来的思路去解决这个问题。

广度优先搜索

广度优先搜索（也称宽度优先搜索，缩写BFS，以下采用广度来描述）是连通图的一种遍历策略。因为它的思想是从一个顶点V0开始，辐射状地优先遍历其周围较广的区域，故而得名。 一般可以用它做什么呢？一个最直观经典的例子就是走迷宫，我们从起点开始，找出到终点的最短路程，很多最短路径算法就是基于广度优先的思想成立的。算法导论里边会给出不少严格的证明，证明过程虽然严谨，但晦涩难懂。不如用大白话讲的清楚明白。在讲广度优先搜索算法之前，需要明白另一件事情，连通图。

连通图的概念

刚刚说的广度优先搜索是连通图的一种遍历策略，那么什么是连通图。在图论中，连通图基于连通的概念。在一个无向图G 中，若从顶点i到顶点j有路径相连（当然从j到i也一定有路径），则称i和j是连通的。如下图

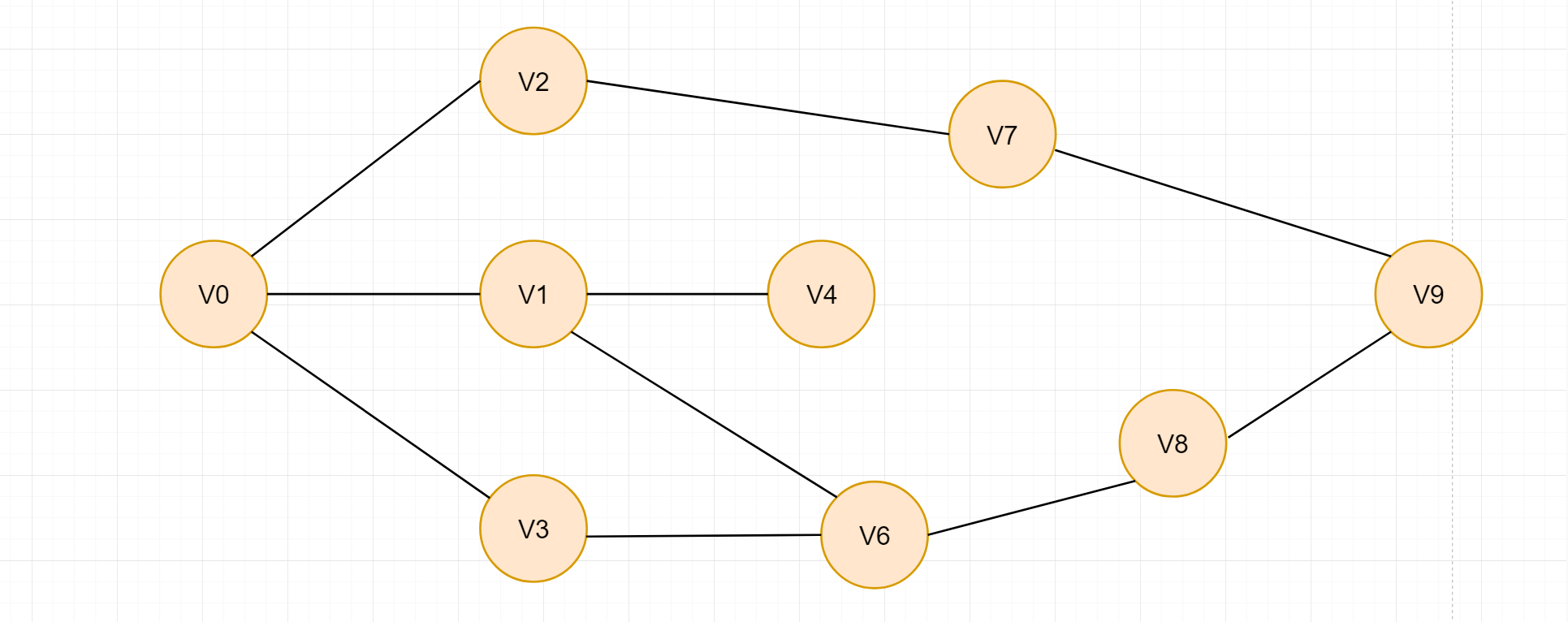
这就是我们所说的连通图，这里展示的是一个无向图，连通即每2个点都有至少一条路径相连。例如V0到V9的其中一条路径就是V0 -> V2 -> V7 -> V9。一般我们把顶点用V缩写，把边用E缩写。

算法的基本思路

在搜索路径时，我们常常需要寻找最短路径，如上图中从 V0到V9一共有如下三条路径 { V0 -> V2 -> V7 -> V9 } , { V0 -> V1 -> V6 -> V8 -> V9 } , { V0 -> V3 -> V6 -> V8 -> V9 }。那么我该怎么找到最短路径 { V0 -> V2 -> V7 -> V9 } 呢。想一想刚刚你是怎么判断出最短路径的，是把到V9的三条路径都找出来了，再判断路径长度，找到最短的吗？看起来刚刚似乎是这么做的，能不能在边找终点的时候边把路径长度也判断了呢。是可以的，我们来看一下如果用广度优先搜索算法从V0到V9是怎么做的：

1. 从V0开始找下一个可以到达的节点，可以找到 [ V2 , V1, V3 ]，和这一个集合中不包含终点 V9，于是进行第二步
2. 分别从第一步中找到的三个节点 V2，V1，V3开始找它们下一个可到达的节点，于是 V2可到达 [ V7 ]，V1可到达 [ V4，V6 ]，V3可到达 [ V6 ]。在三个集合中都不包含终点V9，于是进行第三步
3. 在第二步中找到节点 V7，V4，V6继续寻找下一个可到达节点，V7可到达 [ V9 ] ，V4没有可到达的节点，V6可到达 [ V8 ]。在找到的可到达节点中找到了终点 V9，于是搜索结束

通过刚刚这个搜索过程，其实发现第一二三步操作都是类似的，就是从起始节点开始寻找它下一个可到达节点，有点像辐射形状的搜索方式，从一个节点，向其旁边节点传递病毒，就这样一层一层的传递辐射下去，知道目标节点被辐射中了，此时就已经找到了从起点到终点的路径。这就是广度优先搜索的算法思路，很简单吧，就是这个简单的算法思想能解决大部分求最短路径问题，大道至简。下面用图再画一下算法的思路过程

图解广度搜索算法

我用图来演示广度优先搜索的算法过程，设已走过的节点颜色为黑色，下一个可达节点的颜色为灰色，未走过的节点颜色为白色，已知搜索的起始节点为V0，终止节点为V9。求V0到V9的最短路径。最终最短路径我会用红色表示出来。初始化状态如下图

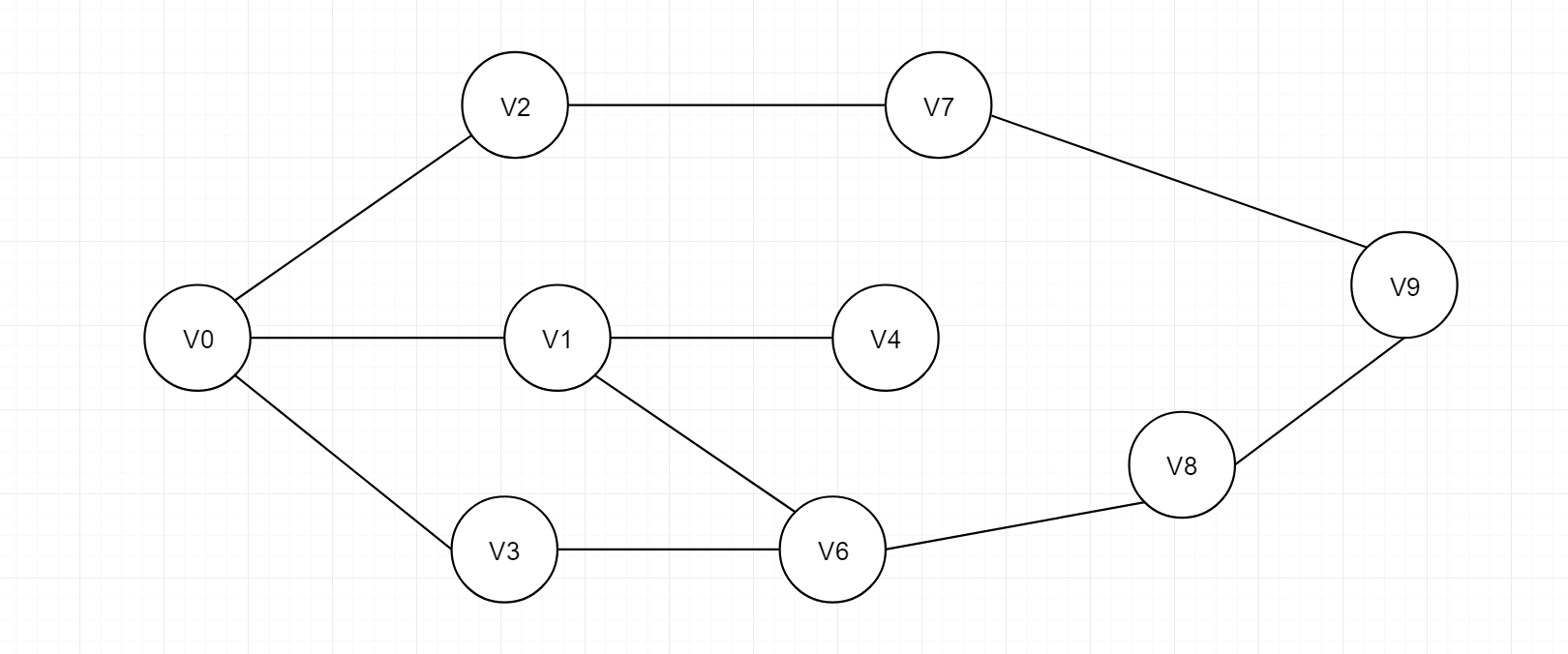
1. 从V0开始搜索，V0置为灰色

   

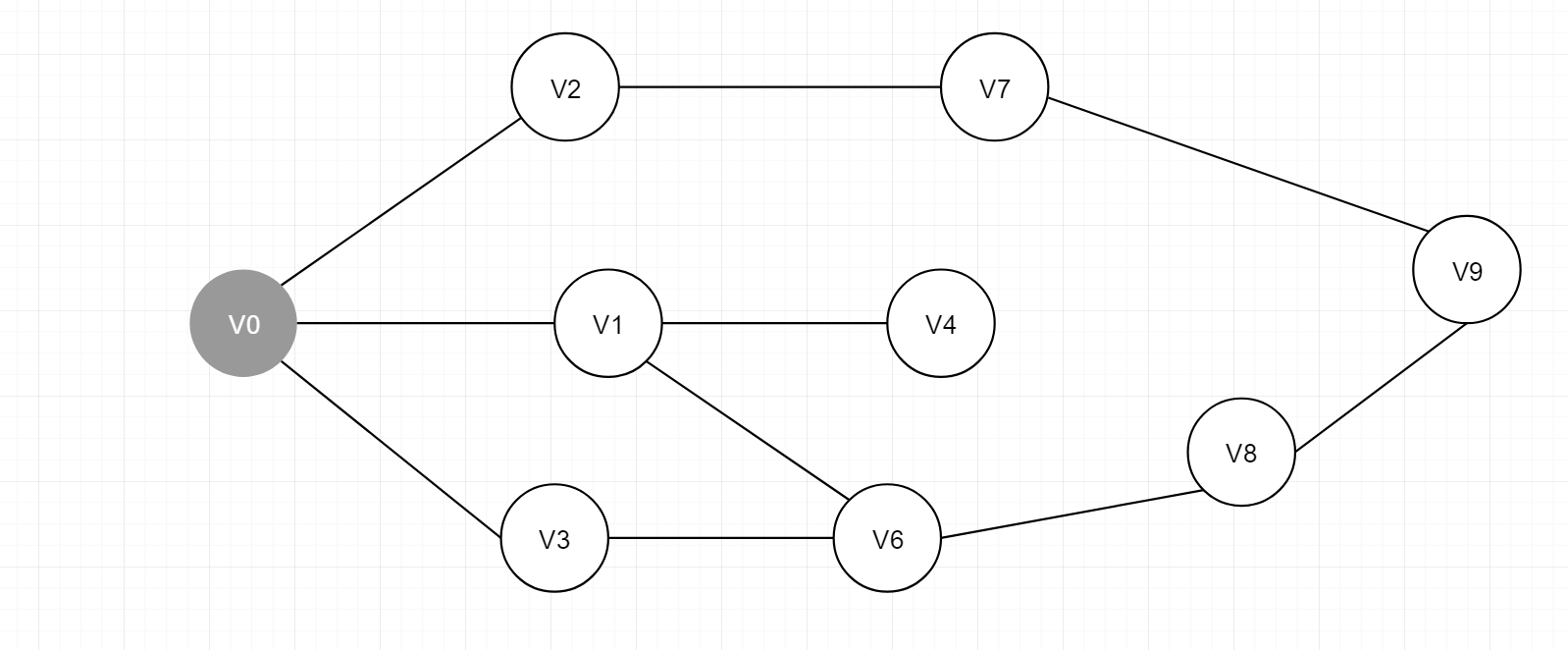
2. V0节点的下一个可达节点集合为 [ V2, V1 , V3 ]，故图下一步操作如下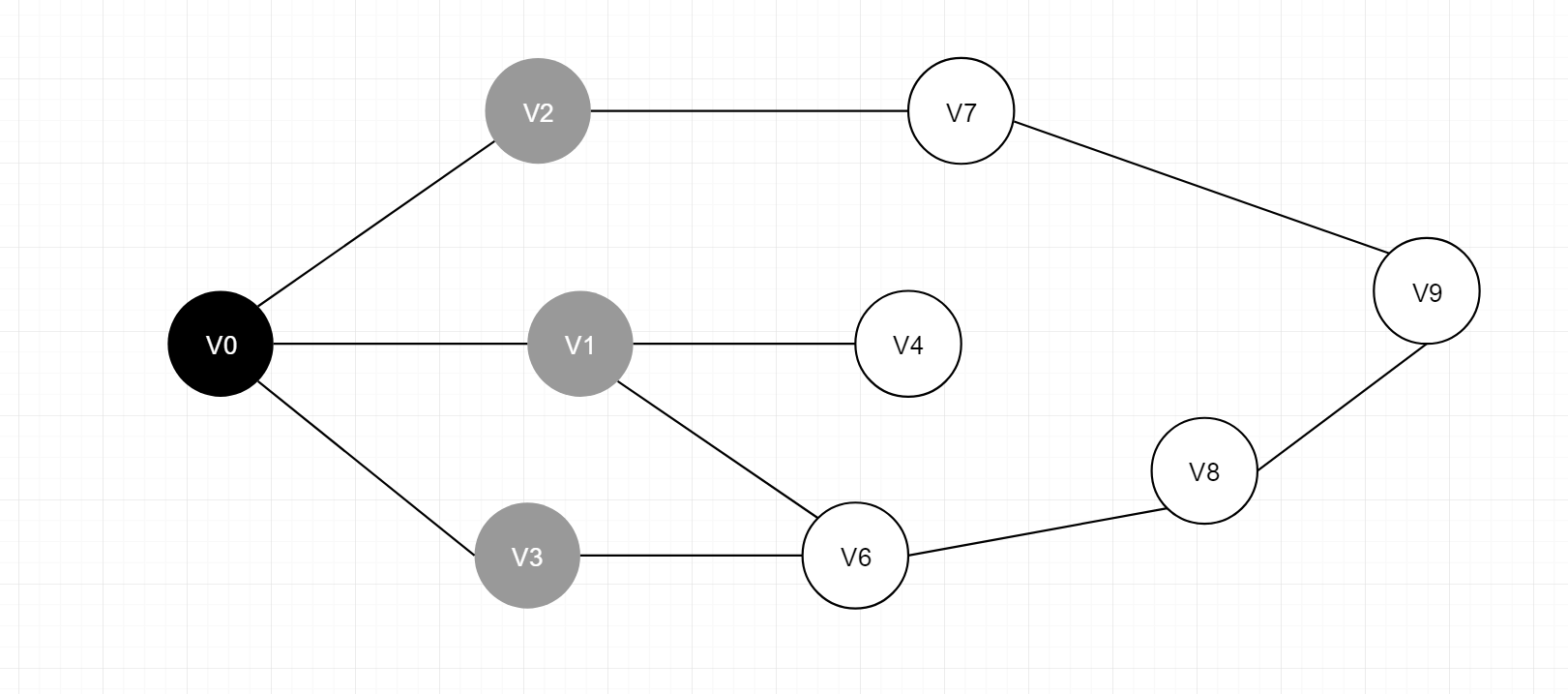

   

3. V1，V2，V3节点的下一个可达节点集合为 [ V4，V6，V7 ]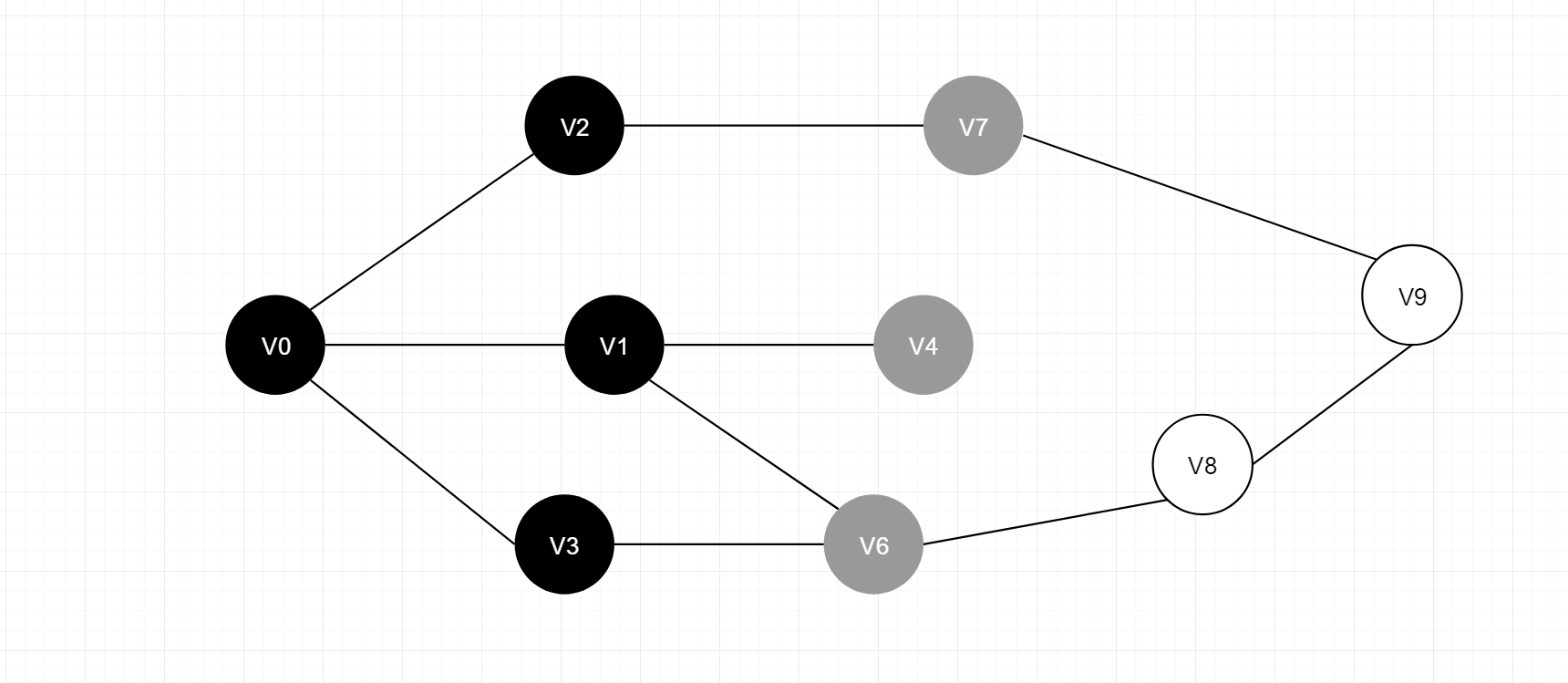

   

4. V4，V6，V7节点的下一个可达节点集合为 [ V8 , V9 ]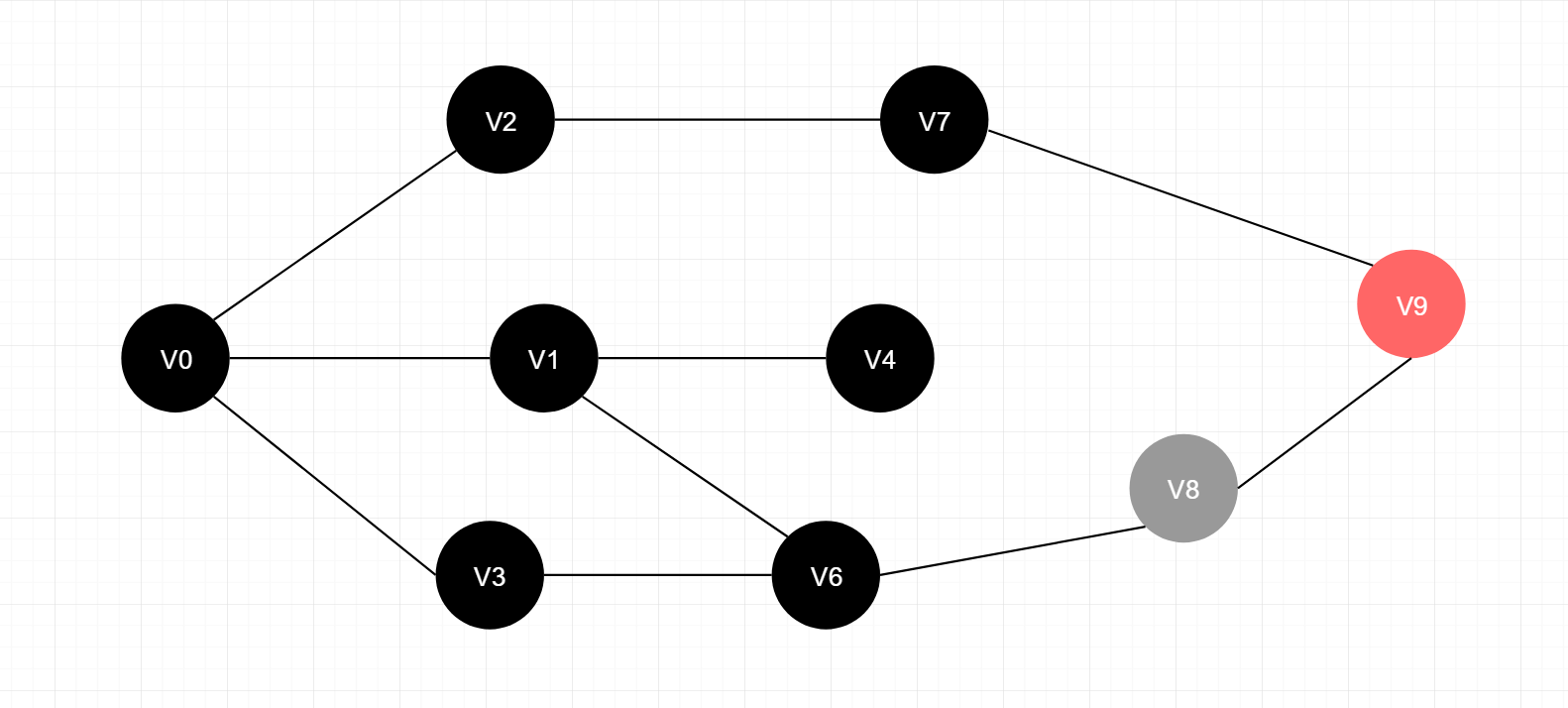

   

5. 这个集合中已经包含终止节点V9，因此搜索结束，最终找到最短路径

   

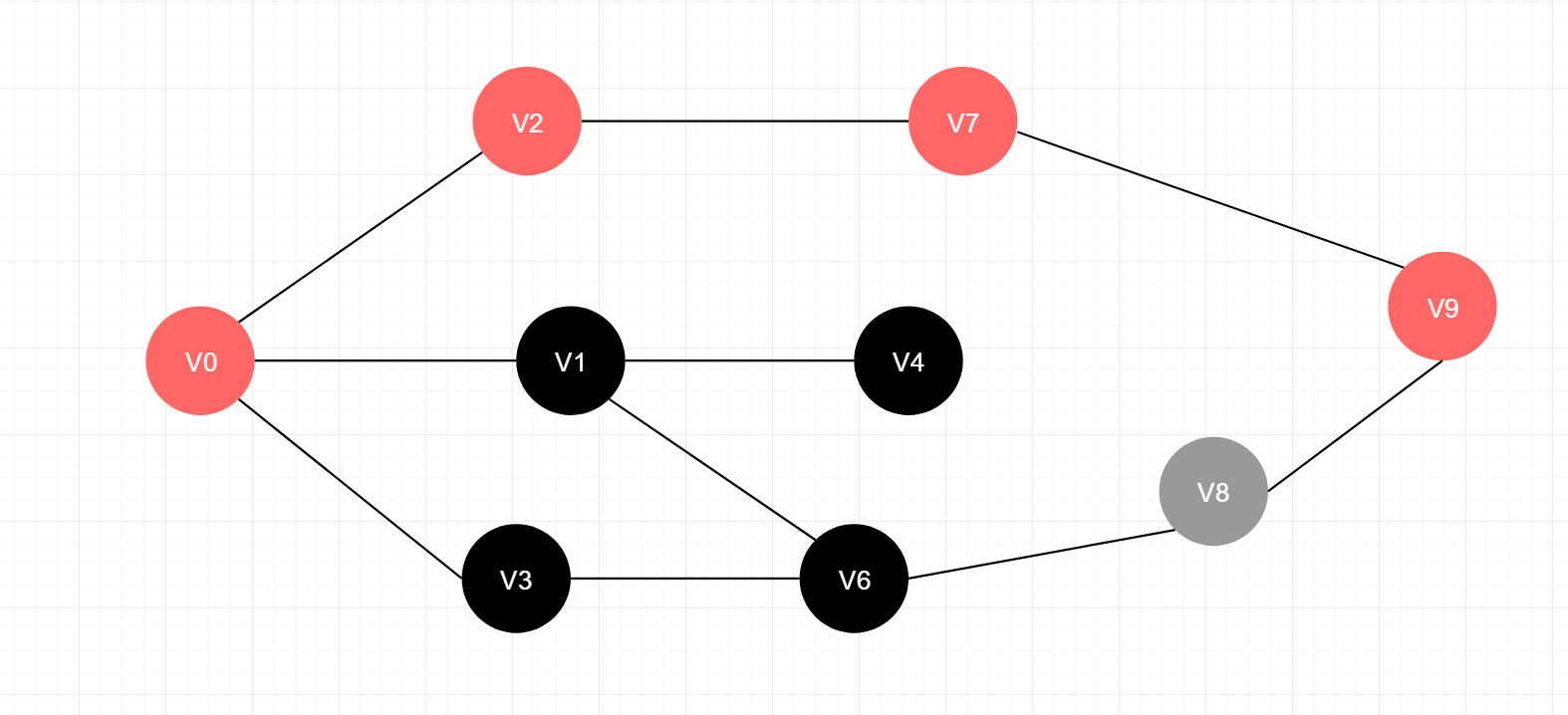
总结

广度优先搜索算法思路很简单，就是从当前节点向外辐射可到达的节点，如此往复，直到辐射到目标节点。对于节点较多的情况，广度优先搜算法会有占内存多的缺点，但速度较快。因此可理解为广度优先算法是以牺牲空间复杂度来换取较快的时间复杂度