最近在阅读一些JS开源组件的源码时,感觉有些吃力。原因在于源码的写法非常娴熟,充分的利用了JS语言函数式的特性,代码老练。虽然我使用JS也有几个年头了,但是仅仅停留在前端页面的一些字段校验和简单逻辑上,没有深入的去理解函数式编程思想。随着近几年函数式编程越来越受到重视,于是决定去学学它的函数式编程思维,与它有相同特性的 Python 也是函数式编程语言,Java8中也引入了函数式编程语言的特性(Java8的Lambda表达式)。我一直觉得学习一样新东西,首先要去了解它的历史,知道来龙去脉才会明白它的背景和价值,才会明白我们为什么要学习它使用它。

起源
现代形式科学的所有的故事都来自于莱布尼茨的两大梦想:一、建立一套严格精密的人工语言,这种语言没有人类语言的歧义多结构,可以精确地描述任何哲学、逻辑和数学问题;二、找到一种方法,利用这套“普遍语言”,解决任何科学、哲学和数学的问题。莱布尼茨的梦想,在20世纪先后成真:集合论和符号逻辑、计算科学。而这一切的一切都源自19世纪末20世纪初发生的第三次数学危机。这场危机的结果使得数学、逻辑学和哲学发生了脱胎换骨的变化,数学的公理化、逻辑学的数学化、哲学的逻辑化是这个伟大变革中最显著的特点。不过很遗憾,这里没有空间详细讲故事,只有三个关键词:数学公理化,数学逻辑化和公理集合论。如果对这段历史不太了解可以参考《数学悖论与三次数学危机》第3、4、5章以及《逻辑的引擎》这两本书。λ演算的创建人是Alonzo Church(中文:阿隆佐·丘奇)。Church1903年生于美国华盛顿特区,后在普林斯顿大学学习数学,专攻数理逻辑。函数编程语言最重要的基础是λ演算。是否存在一个通用模型来解决一切计算任务?1936年,阿隆佐·邱奇设计了一个名为lambda演算的形式系统用来解决这个问题。这个系统实质上是为一个超级机器设计的编程语言。在这种语言里面,函数的参数是函数,返回值也是函数。这种函数用希腊字母lambda(λ),这种系统因此得名。除了阿隆佐,艾伦·图灵也在进行类似的研究。他设计了一种完全不同的系统(后来被称为图灵机),并用这种系统得出了和阿隆佐相似的答案。冯.诺依曼结构实现了理论上的图灵机,并且用在了如今的电脑上。而Alonzo Church的计算模型,与图灵机一样强大,但由于一些历史原因(当时整个世界笼罩在战争的火光和硝烟之中,美国陆军和海军前所未有的大量使用炮弹,为了改进炮弹的精确度,部队组织了大批的科学家持续地计算微分方程以解出弹道发射轨迹。在渐渐意识到这个任务用人力手工完成太耗精力后,开始着手开发各种设备来攻克这个难关。第一个解出了弹道轨迹的机器是 IBM 制造的 Mark I,它重达 5 吨,有 75 万个组件,每秒可以完成三次操作。1949 年,第一台电子离散变量自动计算机EDVAC诞生并取得了巨大的成功。它是冯·诺伊曼设计架构的第一个实例,也是一台现实世界中实现的图灵机。那一年开始好运与阿隆佐·丘奇无缘。)走了上了一条更加学术化,更不商业化的道路。后来人们证明图灵机和 λ 演算能力等同。现在我们使用的家用计算机,服务器基本都是图灵机,图灵也因此被誉为计算机之父
发展
上世纪50年代末,一个叫John McCarthy(约翰·麦卡锡)的MIT教授(他是普林斯顿的硕士)对阿隆佐的成果产生了兴趣。1958年他发明了一种列表处理语言(Lisp),这种语言是一种阿隆佐lambda演算在现实世界的实现,而且它能在冯·诺伊曼计算机上运行!很多计算机科学家都认识到了Lisp强大的能力。1973年在MIT人工智能实验室的一些程序员研发出一种机器,并把它叫做Lisp机。于是阿隆佐的lambda演算也有自己的硬件实现了!传统的程序设计语言是适应冯·诺依曼型计算机系统结构而发展起来的,LISP在诺依曼型计算机上运行的效率要低一些。计算机系统结构的发展,使得函数型语言有着广阔的前途。为了适应当前微型机发展水平和程序员使用传统语言编程的习惯,LISP语言增加了许多非函数型的语言成分,例如,prog、go等函数,所以,LISP已不是纯函数型语言,它既具有函数语言的功能,又具有传统语言的功能。
对比
在函数式语言中,函数(lambda 演算)作为一等公民,可以在任何地方定义,在函数内或函数外,可以作为函数的参数和返回值,可以对函数进行组合。函数式编程中的函数这个术语不是指计算机中的函数,而是指数学中的函数,即自变量的映射。也就是说一个函数的值仅决定于函数参数的值,不依赖其他状态。比如sqrt(x)函数计算x的平方根,只要x不变,不论什么时候调用,调用几次,值都是不变的。与函数式编程对应的是命令式编程(OOP),命令式编程是面向计算机硬件的抽象,有变量(对应存储单元),赋值语句(获取,存储指令),表达式(内存引用和算术运算)和控制语句(跳转指令)。下面是两种编程范式的对比
| 命令式范式(OOP) | 函数式范式(FP) |
|---|---|
| 万物皆对象 (这话并不准确,例如Java中的方法就不能抽象为对象) |
第一等公民是函数 (基本数据类型,如1,2,3也可以用函数表示) |
| 抽象和封装 | 带有闭包的Lambdas/Anonymous函数 |
| 核心活动是组合和对象 | 核心活动是编写新的函数 |
| 着重于数据和状态 | 不变性,大部分无态处理,没有状态和变量 |
| 基于图灵机 | 基于λ演算 |
面向对象和面向函数一直在争论,实际上纯粹的OOP和纯粹的FP都是极端的。
- 对于OOP来讲:存在的并一定都是对象,函数就不是对象
- 对于FP来说:存在的并不总是纯粹的,副作用总是真实存在
函数式中将超过计算的东西叫做副作用,因为文件读写,打印,随机数,这些东西都不是纯的计算过程,而是涉及到外部世界的交互,依赖于机器,不在理论的范畴。这些是不可避免的,因此副作用总是真实存在的。
lambda | λ演算 定义
在lambda演算中只有三种合法表达式(也可以称之为项:λ-expression or λ-term)存在,λ演算是一个为了表达和计算函数的形式化系统,有着自己的化简规则和语法。整个系统是基于表达式的(也叫λ项)。一个表达式可以是一个变量(variable),一个抽象体(abstraction)或者一个应用(application)。即
expression = variable || abstraction || application 变量(Variable)
形式:x ,变量名可能是一个字符或字符串,它表示一个参数(形参)或者一个值(实参)。如果 X 是变量,E 是表达式,则λx.E是一个抽象体。
variable = expression抽象(Abstraction)
形式:λx.M,在λ演算中,函数是用λ表示的匿名函数。一个匿名函数中只存在标识符和他自己的函数体。例如λx.x表达式定义了一个函数(也叫做λ抽象体)。紧跟在λ后面的名字是参数标识符,点后面的表达式是函数体。我们用javascript表示它:
function (x) {
return x
} λx.y表示一个常量函数(constant function),输出恒为y与输入无关。抽象体的通用模板
abstraction = λ(variable).(expression) 应用(Application)
形式:M N,它表示将函数M应用于参数N,其中M、N均为合法lambda表达式。简单来说就是给函数M输入实参N。例如(λx.x) y, (λx.x) (λx.x)。前者表示将函数λx.x应用于变量y,得到y;后者表示将函数λx.x应用于λx.x,得到λx.x。函数λx.x是一个恒等函数(identity function),即输入恒等于输出
application = (expression)(expression) 注意,这时候可能就有人纳闷儿了,(λx.x) y意义很明确,但λy.xy为什么代表函数抽象而不是将函数λy.x应用于y的函数应用呢?为了消除类似的表达式歧义,可以多使用小括号,也有以下几个消歧约定可以参考:
- 一个函数抽象的函数体将尽最大可能向右扩展,即:
λx.M N代表的是一个函数抽象λx.(M N)而非函数应用(λx.M) N。 - 函数应用是左结合的,即:
M N P意为(M N) P而非M (N P)
柯里化(Currying)
有时候我们的函数需要有多个参数,这太正常不过了,但是lambda函数只能有一个参数怎么办?解决这个问题的方法就是柯里化(Currying)。柯里化是用于处理多参数输入情况的方法,我们已经知道一个lambda函数的输入和输出也可以是函数,那么基于它,可以把多参数函数和单参数函数做以下转换:
currying: λx y.xy = λx.(λy.xy)外层函数接受一个参数x返回一个函数λy.xy,这个返回函数(内层函数)又接受一个参数y返回xy,x绑定于外层函数,y绑定于内层函数,这样我们就在满足lambda函数只接受一个参数的约束下实现了多参数函数的功能,这就是柯里化,而λx y.xy称为λx.(λy.xy)的缩写,为了方便表达,后续会常常出现λx y.xy这样的书写方式,需要谨记它只是缩写写法。
lambda | λ 归约
beta | β 归约
对于一个函数应用(λx.x) y,它意为将函数应用λx.x应用于y,等价于x[x:=y],即结果是y。在这个过程中,(λx.x) y ≡ x[x:=y]一步就叫做beta归约,x[x:=y] ≡ y一步称作替换(substitution),[x:=y]意为将表达式中的自由变量x替换为y。
替换:形式:E[V := R],意为将表达式
E中的所有 “自由变量”V替换为表达式R。对于变量x,y和lambda表达式M,N,有以下规则:x[x := N] ≡ N y[x := N] ≡ y //注意 x ≠ y (M1 M2)[x := N] ≡ (M1[x := N]) (M2[x := N]) (λx.M)[x := N] ≡ λx.M //注意 x 是绑定变量无法替换 (λy.M)[x := N] ≡ λy.(M[x := N]) //注意 x ≠ y, 且表达式N的自由变量中不包含 y 即 y ∉ FV(N)beta归约:形式:β: ((λV.E) E′) ≡ E[V := E′],其实就是用实参替换函数体中的形参,也就是函数抽象应用(apply)于参数的过程啦,只不过这个参数除了是一个变量还可能是一个表达式。
细心的话可以注意到,替换规则中特别标注了一些x ≠ y或者y ∉ FV(N)等约束条件,它们的意义在于防止lambda表达式的归约过程中出现歧义。比如以下过程:
// 错误演算
(λx.(λy.xy)) y
= (λy.xy)[x:=y] //beta归约:注意 y ∈ FV(y) 不满足替换的约束条件
= λy.yy //替换:绑定变量y与自由变量y同名出现了冲突可以看出在不满足约束条件的情况强行替换造成了错误的结果,那么对于这种情况该如何处理呢?那就需要alpha转换啦。
alpha | α 转换
这条规则就是说,一个lambda函数抽象在更名绑定变量前后是等价的,即: α: λx.x ≡ λy.y,其作用就是解决绑定变量与自由变量间的同名冲突问题。那么对于上面的那个错误归约过程就可以纠正一下了
(λx.(λy.xy))y
= (λy.xy)[x:=y] //beta归约:注意 y ∈ FV(y) 不满足替换的约束条件
= (λz.xz)[x:=y] //alpha转换:因为绑定变量y将与自由变量x(将被替换为y)冲突,所以更名为z
= λz.yzeta | η 归约
灵活运用alpha和beta已经可以解决所有的lambda表达式归约问题,但是考虑这样一个表达式:λx.M x,将它应用于任意一个参数上,比如(λx.M x) N,进行beta归约和替换后会发现它等价于M N,这岂不是意味着 λx.M x ≡ M。没错,对于形如λx.M x,其中表达式M不包含绑定变量x的函数抽象,它是冗余的,等价于M,而这就是eta归约,它一般用于清除lambda表达式中存在的冗余函数抽象。
邱奇数
Church 编码是把数据和运算符嵌入到 lambda 演算]内的一种方式,最常见的形式是 Church 数,它是使用 lambda 符号的自然数的表示法。这种方法得名于 Alonzo Church,他首先以这种方法把数据编码到 lambda 演算中。在其他符号系统中通常被认定为基本的项(比如整数、布尔值、有序对、列表和 tagged unions)都被映射到使用 Church 编码的高阶函数;根据邱奇-图灵论题我们知道任何可计算的运算符(和它的运算数)都可以用 Church 编码表示。Church 数 0, 1, 2, … 在 lambda 演算中被定义如下:
0 ≡ λf.λx. x
1 ≡ λf.λx. f x
2 ≡ λf.λx. f (f x)
3 ≡ λf.λx. f (f (f x))
...
我们可以使用js来验证这个计算模型
'use strict';
// 定义数字0:
// 定义数字0:
let zero = function (f) {
return function (x) {
return x;
}
};
// 定义数字1:
let one = function (f) {
return function () {
return f();
}
};
// 计算数字2 = 1 + 1:
let two = add(one, one);
// 定义加法:
function add(n, m) {
return function (f) {
return function () {
return m(f)(n(f)());
}
}
}
// 计算数字3 = 1 + 2:
let three = add(one, two);
// 给3传一个函数,会打印3次:
three(function () {
console.log('print 3 times');
})();
// 计算数字5 = 2 + 3:
let five = add(two, three);
// 给5传一个函数,会打印5次:
five(function () {
console.log('print 5 times');
})();
运行结果如下
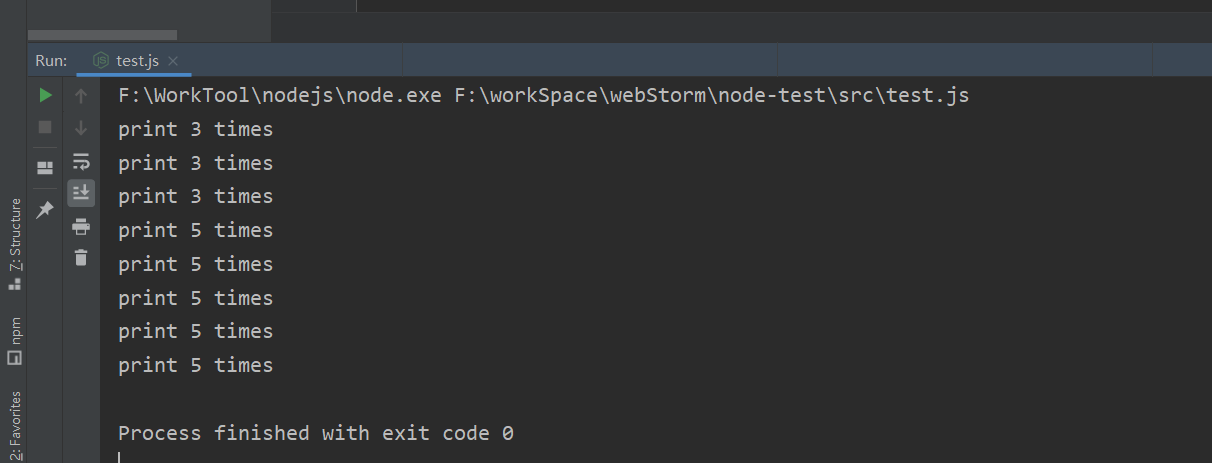
实现原理实际上这里打印的次数,就是函数被调用的次数,邱奇用函数的递归调用次数来表示基本数据。
总结
在函数式编程的世界中,一切皆函数,函数是一等公民。一等公民这个名字听起来很高大上,但是也相当晦涩,这个词也不是翻译的不好,因为英文原文中叫first class citizen很多人包括我也不知所云。其实所谓一等公民,它的意思是函数与基本数据类型一样,可作为函数的入参,也可作为函数的返回值,函数可以赋值给变量。我们知道在平常的命令式编程语言中(例如Java)中,函数的返回值比较简单,只能是基本数据类型(整型,布尔,字符串等)或者是一个Object。而在JavaScript函数是第一公民,因此我们也可以在函数中返回函数。正因为有了这种属性,函数的入参可以是函数,函数的返回值可以是函数,于是便有了高阶函数,以及各种骚操作和一些看起来很炫酷的语法糖。可以说函数为第一公民是函数式编程的必要条件。



