Paxos算法是莱斯利·兰伯特(Leslie Lamport,就是 LaTeX 中的”La”,此人现在在微软研究院)于1990年提出的一种基于消息传递且具有高度容错特性的一致性算法。 Paxos算法应用非常广泛,目前在Google的Chubby、MegaStore、Spanner等系统中得到了应用,Hadoop中的ZooKeeper中实现数据的一致性也是基于Paxos算法。根据 CAP 理论,一个分布式集群中网络分区必然会出现,这样就会出现脑裂的情况,所谓脑裂,就是由于网络分区的出现,一个集群被分割为多个互不通信的小集群,小集群中由于没有Leader,会自主选择master节点,造成原本的集群会同时存在多个master节点。 而 paxos 算法有效的杜绝了脑裂现象,并在 C 和 A 之间保留了较好的均衡性。因此paxos算法的重要性不言而喻了,但Paxos 算法号称史上最晦涩难懂的算法,而原版论文也是让人难以理解 。经过一段时间学习,对 Paxos 有了一些理解,在这里总结一下。paxos算法的学习最好的资料就是作者发表的三篇论文,分别是Fast Paxos,Paxos made simple和The Part-Time Parliament。另外还有一个被称为有史以来学习paxos最好的地方的英文网站,百度网盘地址如下:
Fast Paxos:链接: https://pan.baidu.com/s/1Eaxpvh5AqUNyxySPAOrwYQ 密码: ij5v
Paxos made simple:链接: https://pan.baidu.com/s/1rBjQ4rXnBWO1hXdOllGguw 密码: k7fj
The Part-Time Parliament:链接: https://pan.baidu.com/s/18SZs710g_VAPoM1wbijHnQ 密码: ww4w
英文学习网址:Paxos (computer science)

1 . Paxos算法
1.1 Paxos算法的角色
Client:客户端,发起请求并等待返回。
Proposer:提案发起者,处理客户端请求,将客户端的请求发送给Acceptor,并接收Acceptor返回的信息
Acceptor:提案决策者,负责处理接收到的提案,决策提议通过还是拒绝,并把信息返回给Proposer
Learner:当有同一个提案的值被超过一半的Acceptor采纳并发送消息给Learner时,Learner学习该提案值。
其实最核心的角色就两个,分别是Proposer 和 acceptor。
2.2 Paxos算法流程
简单来说Paxos 是一个经典的两阶段提交(2PC)
2.2.1、第一阶段 Prepare
Proposer 发送提案,发送提前前需生成生成全局唯一且递增的提案 ID(Proposalid,以高位时间戳 + 低位机器 IP 可以保证唯一性和递增性),向 Paxos 集群的所有机器发送 PrepareRequest请求,这里无需携带提案内容,只携带 Proposalid 即可。Acceptor在接收到Proposer发来的提案后需要做几件事情,总结来说就是:两个承诺,一个应答 。
两个承诺:
- 第一,不再应答 Proposalid 小于当前请求的 PrepareRequest。
- 第二,不再应答 Proposalid 小于当前请求的 AcceptRequest 。
一个应答:
- 返回自己已经采纳的提案中 Proposalid 最大的那个提案的内容,如果没有则返回空值;。
2.2.2、第二阶段 Accept
经过第一阶段,Proposer会收到Acceptor的应答。这时Proposer也需要做几件事情。总结来说就是:三个判断,一个请求。注意只有应答数过半才会发送AcceptRequest 请求。
两个判断:
- 第一,判断收到的Acceptor的应答数量超过总数的一半,如果没有超过一半则直接进入第一阶段的流程,继续发送提案。如果超过一半,则进入第二个判断。
- 第二,判断所有返回Acceptor的应答中是否存在已经采纳的提案,如果不存在则自己决定提案值,如果存在提案值则进入第三个判断。
- 第三,判断应答的所有提案中,是否存在数量超过一半的提案,如果存在则选中这个过半数的提案值,如果不存在则在所有Acceptor的应答中选中Proposalid最大的提案值。
一个请求:
- 发送AcceptRequest 请求,将决定的提案值发送给Acceptor,然后会得到Acceptor的应答,根据应答数量再走第二阶段的流程。
Learner学习被选定的Value值(也就是提案值)。假设集群中有M个Acceptor,N个Learner,那么Learner学习的策略有三种方案:
- Acceptor接受一个提案,就将该提案发送给所有Learner。优点是Learner能快速获取被选定的Value值,缺点是通信次数为:M*N
- Acceptor接受一个提案,就将该提案发送给主Learner,主Learner再发送给其他的Learner。优点是通信次数只有:M+N,缺点是主Learner会出现单点故障,而且主Learner怎么选举来的也是个问题。
- Acceptor接受一个提案,就将提案发送给多个Learner,也就是一个Learner集合。再由这个Learner集合发送给剩下的Learner。优点是综合了方案一和方案二,减少了通信次数的同时提高了可靠性。缺点是网络通信更复杂。
可以看出Paxos的关键所在是Proposer的决策,在收到Acceptor的应答后,会选出应答中最新的决策,然后服从该决策,后者认同前者,最后Acceptor接受的同一个提议的数量会越来越多,最终超过一半,达成一致,否则整个决策过程永无止境 。在分布式系统中,上面提到的几种角色并不需要在不同节点上,实际上一个节点既可以是Proposer,也可以是Acceptor只是各自对应的端口不一样就行了,zookeeper就是这样做的。上面两个阶段是分开描述的,可能不便于理解整个连贯的流程。下面以生活中的实际场景来模拟一下paxos算法的流程。
2 . 通俗理解
相信大家都参与过班级中竞选班长的场景。班长竞选流程一般是首先竞选者上台演讲,演讲结束后,大家同意投票,比如没人写个小纸条,在纸条上,我想选谁当班长就写他的名字。最后由老师或是一个同学数纸条上的名字数最多的人当选班长。这种方式其实就是数据共享的方式,因为所有人的小纸条都聚集在了一起,最后只要数这些小纸条就行了。但Paxos算法不是这种场景 ,Paxos算法的场景对应一种分布式场景。假设这个班级有20个人要竞选一名班长,而这20个同学不在教室,而各自在家且这20个同学相互不能通信如何完成班长的选举。为了完成班长的选举,他们请来了隔壁班的5位同学,且这5位同学也不能相互通信。但20位同学中的每个人都可以自由的和隔壁班的这5位同学通信,现假设他们通信的方式为短信,隔壁班的5位同学称他们为队长,20位同学为队员。下面宣布选举开始!
首先队员的第一件事就是与至少3个队长取得联系(超过队长人数的一半,为什么要超过人数的一半,后面我会解释),于是队员们开始疯狂的给5位队长发短信,队员发送信息时,会把当前的信息的发送时间一起发过去,这个时候队员仅仅只是为了与队长取得联系,并不会把班长竞选人的名单发送过去。队长会收到来自20名队员的短信,面对大量的短信,队长的做法是倾听最新的声音,于是队长只回复信息中发送时间最新的队员。这里队长如果接受过队员的班长人选提议,就会把那个提议回复给这个队员,如果没有接受过提议,就会回复队员:“我还没有班长人选的名字,快告诉我你要选谁当班长”。这时队员a在接收到队长的回复后,并不会马上就把自己的班长人选发送给队长。队员a首先会判断我收到的队长回复人数有没有超过一半,如果没有那我就继续发申请,联系队长。如果超过了一半就看看班长回复的信息中,是不是已经有一些班长人选的名单了,如果没有,那么队员a想选赵六当班长,就会把赵六发送给所有队长。如果有了那么队员a会服从队长的班长人选,队员会归纳队长返回的信息,可能会出现下面两种情况,第一种情况:
队长a的信息:班长人选名字是张三,时间是6分钟前;
队长b的信息:班长人选名字是张三,时间是4分钟前;
队长c的信息:班长人选名字是张三,时间是3分钟前;
队长d的信息:班长人选名字是李四,时间是1分钟前;
队长e的信息:没有班长人选,时间是1分钟前;
如果出现了这种情况,那就别扯了,说明整个决定过程已经达成一致了,张三已经当选班长,队员a也选张三做班长。这里还会出现第二种情况,就是决定过程还没有达成一致,收到的信息如下:
队长a的信息:班长人选名字是李四,时间是3分钟前;
队长b的信息:班长人选名字是李三,时间是5分钟前;
队长c的信息:没有班长人选,时间是1分钟前;
没有收到队长d和队长e的信息
这时队员a就会选择队长a的班长人选名字,即李四,并把这个名字发送给所有队长,告诉他们李四就是我想要选的班长。
从这面的逻辑可以看出,一旦某个时刻有半数以上队长同意了一个班长人选比如张三,紧跟着后面的队员b继续发短信时,如果和队长们获得联系,说明队员b收到了来自半数以上队长发过来的消息,那么队员b必然会收到至少一个队长给他发的张三的这个结果,于是队员b也会顶这个最新的班长人选,不会更改。其他队员也是一样,因为最终都会与队长取得联系,而此时队长最新的人选是张三,于是会有越来越多的人支持张三,最终达成一致,张三当选班长。这里就是paxos算法的根基,因为每个队员必须受到半数以上的回复才能参与班长人选的提议,虽然每个队员受到回复的队长可能不一样,但是因为超过半数,所以他们必然有一个交集,两个交集必然有一个共同的提议。因此最终肯定能达成一致。光这样说有些难以理解,来举个栗子,看下图:
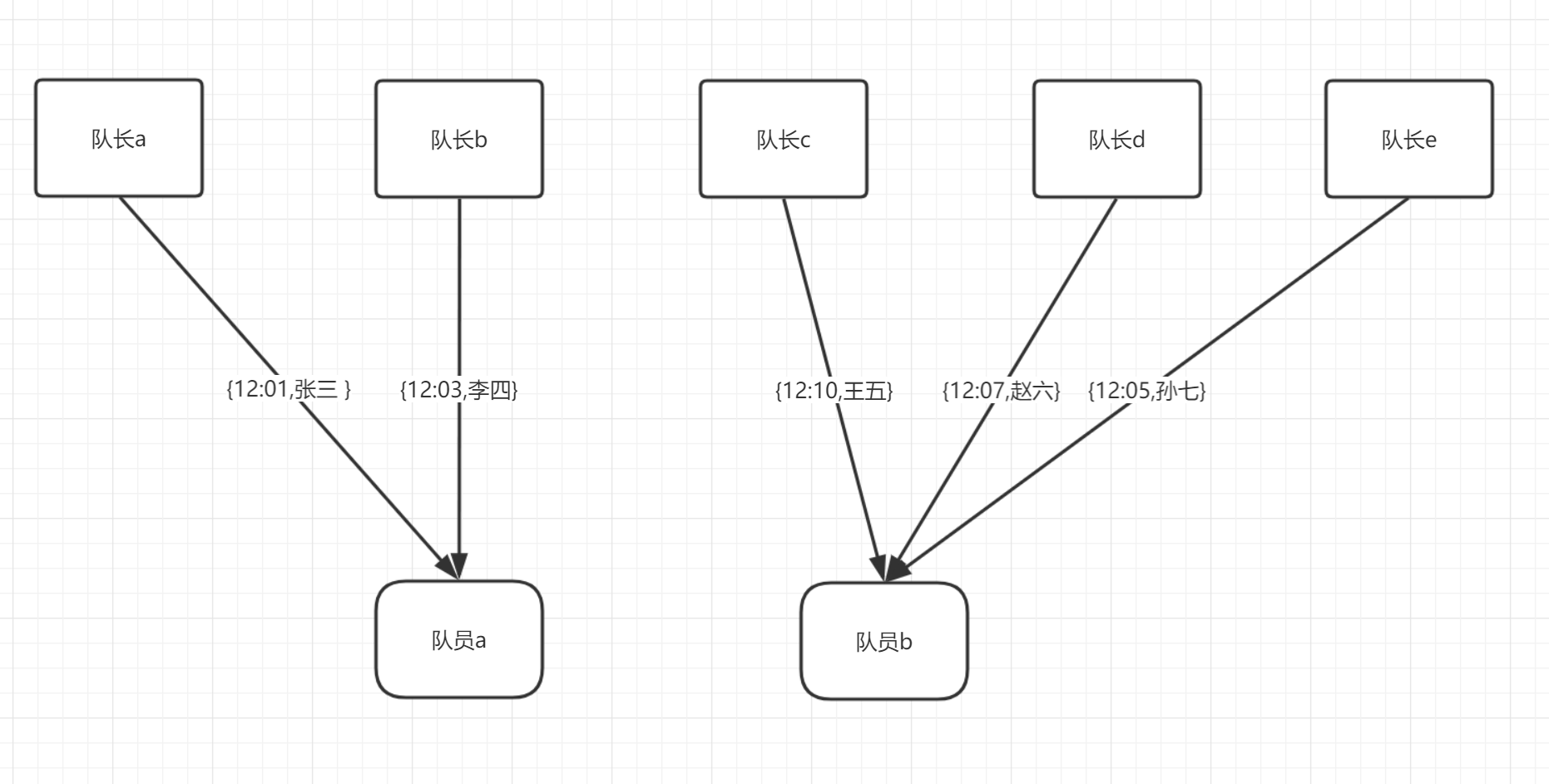
如果队员不需要受到过半的回复就可以进入第二阶段参与班长人选的提议,如上图中,队员a收到两位队长的回复分别是队长a的班长人选12点01分的张三,队长b的12点03分的李四,队员b收到三位队长的回复分别是12点10分的王五,12点07分的赵六,12点05分的孙七。那么根据前面的逻辑,队员a会选李四当班长,队员b会选王五当班长,然后再把信息发给队长们。由于两个队员收到的回复没有交集,因此他们两个的班长人选名字永远都不可能相同,队长们的信息永远是不一致的,所以永远都不可能有班长人选的名字超过半数。这样会导致选举过程永无止境,陷入死循环。而如果队员必须收到半数以上的回复才能参与提议,情况会变成什么样的呢?,看下图:
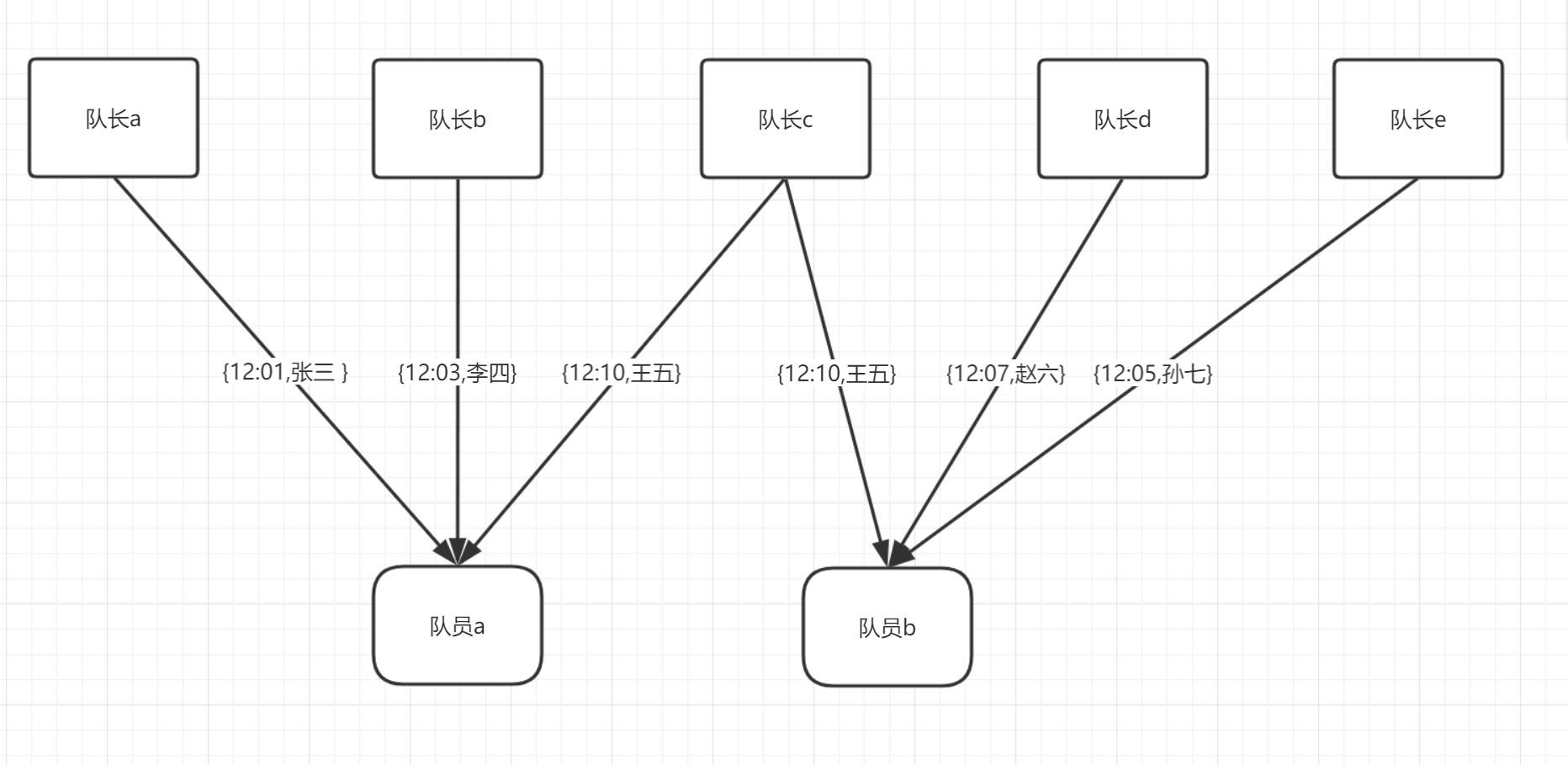
这个图中两名队员都收到了过半的队长回复,由图可以很明显的看出,队员a和队员收到的回复中是存在交集的,根据前面的逻辑队员a会选王五当班长,队员b会选王五当班长。队员们会把自己选择的班长人选名单发送给队长们,于是在所有队长那里王五都成了最新的班长人选,所以队长都会接受。在接下来其他队员与队长们取得联系后返回的班长人选中必然包含王五,这样支持王五的人会越来越多,最终达成一致。
有人可能会疑问,虽然只是举个例子,但这里为什么只考虑队员a和队员b的情况,万一其他队员得到的信息能使选举最终达成一致呢?这里下意识的用了万一这个词,仔细想想这个词又不得不用,因为刚刚这个例子就出现导致队长们无法使选举达成一致的情况,那谁又能保证其他队员收到的信息能使队长们最终达成一致呢。我们要的结果是队长们最终肯定能达成一致,而不是万一能达成一致。因此,队员们必须受到半数以上的回复才能并参与提议,才能实现最终的一致性。用数学上的说法就是,只有保证了这个约束条件才保证了paxos算法是一个收敛函数。把例子和理论对应一下,在竞选班长的例子中的队长就相当于paxos算法种的Acceptor,而队员就相当于Proposer和Learner。在选举过程中,队员既会提交选举的提案,也会根据队长返回的信息来学习被选中的人选。
在分布式系统中,一致性的问题一直是个拦路虎。Paxos解决这一问题利用的是选举,少数服从多数的思想,只要2N+1个节点中,有N个(不包含N)以上同意了某个决定,则认为系统达到了一致,并且按照Paxos原则,最终理论上也达到了一致,不会再改变。这样的话,客户端不必与所有服务器通信,选择与大部分通信即可;也无需服务器都全部处于工作状态,有一些服务器挂掉,只有保证半数以上存活着,整个过程也能持续下去,容错性相当好。因此,说ZooKeeper 要部署奇数个节点也是有道理的。另外谈到Paxos时,还会涉及到拜占庭将军问题,拜占庭将军问题指的是在存在消息丢失的不可靠信道上试图通过消息传递的方式达到一致性是不可能的。注意拜占庭将军问题中描述的不可靠信道是指信息可能会丢失,也可能会被篡改。Paxos本身就是利用消息传递方式解决一致性问题的,所以它的假定是信道必须可靠,这里的可靠,主要指信息可以丢失,但不会被篡改。



